
【题目】如图①,在△ABC中,AC=BC,点D为BC的中点,DE⊥AB,垂足为点E,过点B作BG∥AC交DE的延长线于点G.
(1)求证:DB=BG;
(2)当∠ACB=90°时,如图②,连接AD、CG,求证:AD⊥CG。

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)利用平行线的性质,和三角形全等得出结论;(2)利用三角形全等和等角的余角相等,解决问题.
试题解析:证明:(1)∵AC=BC ∴ ∠A=∠CBA
∵ AC∥BG ∴ ∠A=∠GBA即∠CBA=∠GBA
∵ DE⊥AB ∴ ∠DEB=∠GEB
在△DBE和△GBE中
∴ △DBE≌△GBE
∴DB=BG

(2) ∵ 点D为BC的中点 ∴ CD=DB
∵ DB=BG ∴ CD=BG
∵ AC∥BG ∴ ∠ACB+∠GBC=180°
∵ ∠ACB=90° ∴∠GBC=∠ACB=90°
在△ACD和△CBG中

∴ △ACD≌△CBG
即∠CAD=∠BCG
∵ ∠ACG+∠BCG=90°
∴ ∠ACG+∠CAD=90°即 AD⊥CG


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在研究圆的有关性质时,我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合”.由此说明( )
A. 圆是中心对称图形,圆心是它的对称中心
B. 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
C. 圆的直径互相平分
D. 垂直弦的直径平分弦及弦所对的弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③中,点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.
(1)分别求图①,图②和图③中,∠APD的度数.
(2)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答
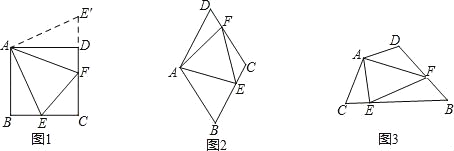
习题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
解:
∵正方形ABCD中,AB=AD,∠BAD=∠ADC=90°
∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.
∴∠E′AF=90°-45°=45°=∠EAF.
又∵AE′=AE,AF=AF
∴△AE′FF≌△AEF(SAS)
∴EF=E′F=DE′+DF=BE+DF.
习题研究.
观察分析:
观察图1,由解答可知,该题有用的条件是①.ABCD是四边形,点E、F分别在边BC、CD上;②.AB=AD;③.∠B=∠D=90°∠;④.∠EAF=![]() ∠BAD.
∠BAD.
类比猜想:
在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B=∠D时,还有EF=BE+DF吗?
要解决上述问题,可从特例入手,请同学们思考:如图2,在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?试证明.
(2)在四边形ABCD中,点E、F分别在边BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=![]() ∠BAD时,还有EF=BE+DF吗?使用图3证明.
∠BAD时,还有EF=BE+DF吗?使用图3证明.
归纳概括:
反思前面的解答,思考每个条件的作用,可以得到一个结论“EF=BE+DF”的一般命题: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻补角是( )
A. 和为180°的两个角
B. 有公共顶点且互补的两个角
C. 有一条公共边相等的两个角
D. 有公共顶点且有一条公共边,另一边互为反向延长线的两个角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列多项式分解因式,结果中不含因式x﹣1的是( )
A. x2﹣1 B. x(x﹣2)+(2﹣x) C. x2﹣2x+1 D. x2+2x+1
查看答案和解析>>
科目:初中数学 来源: 题型:
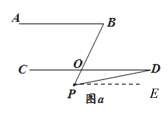
【题目】(1)如图 a,若 AB∥CD,点 P 在 AB、CD 外部,则∠BPD、∠B、∠D 之间有何数量关系?
把下面的解答填上根据:
解:∠B=∠BPD+∠PDC.
理由:作PE∥AB
∵ AB∥CD ( )
∴AB∥CD∥PE ( )
∴∠B=∠BPE, ∠D=∠DPE ( )
∵∠BPE=∠BPD+∠DPE
∴∠B=∠BPD+∠PDC ( )
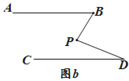
(2)若AB∥CD,将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D 之间有何数量关系?请证明你的结论.
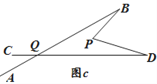
(3)在图 b 中,将直线 AB 绕点B逆时针方向旋转一定角度交直线 CD 于点 Q,如图 c,则∠BPD、∠B、∠D、∠BQD 之间满足的数量关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com