
ЗжЮі ИљОнЪЕЪ§ЕФЗжРрЃЌМДПЩНтД№ЃЎ
НтД№ НтЃК|-0.2|=0.2ЃЌ-ЃЈ-1.3ЃЉ=1.3ЃЎ
е§Ъ§МЏКЯ{+$\frac{1}{3}$ЃЌІаЃЌ|-0.2|ЃЌ-ЃЈ-1.3ЃЉ}
ИКЪ§МЏКЯ{-2ЃЌ-0.3ЃЌ-3.14ЃЌ-7$\frac{1}{3}$}
гаРэЪ§МЏКЯ{-2ЃЌ+$\frac{1}{3}$ЃЌ-0.3ЃЌ0ЃЌ-3.14ЃЌ-7$\frac{1}{3}$ЃЌ|-0.2|ЃЌ-ЃЈ-1.3ЃЉ}
ЗжЪ§МЏКЯ{+$\frac{1}{3}$ЃЌ-0.3ЃЌ-3.14ЃЌІаЃЌ-7$\frac{1}{3}$ЃЌ|-0.2|ЃЌ-ЃЈ-1.3ЃЉ}ЃЎ
ЙЪД№АИЮЊЃК+$\frac{1}{3}$ЃЌІаЃЌ|-0.2|ЃЌ-ЃЈ-1.3ЃЉЃЛ-2ЃЌ-0.3ЃЌ-3.14ЃЌ-7ЃЛ-2ЃЌ+$\frac{1}{3}$ЃЌ-0.3ЃЌ0ЃЌ-3.14ЃЌ-7$\frac{1}{3}$ЃЌ|-0.2|ЃЌ-ЃЈ-1.3ЃЉЃЛ+$\frac{1}{3}$ЃЌ-0.3ЃЌ-3.14ЃЌІаЃЌ-7$\frac{1}{3}$ЃЌ|-0.2|ЃЌ-ЃЈ-1.3ЃЉЃЎ
ЕуЦР БОЬтжївЊПМВщСЫЪЕЪ§ЕФЗжРрЃЎЪЕЪ§ЗжЮЊЃКгаРэЪ§КЭЮоРэЪ§ЃЎгаРэЪ§ЗжЮЊЃКећЪ§КЭЗжЪ§ЃЛЮоРэЪ§ЗжЮЊЃКе§ЮоРэЪ§ЁЂИКЮоРэЪ§ЃЈЮоЯоВЛбЛЗаЁЪ§ЃЉЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
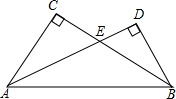 ШчЭМЃЌдкRtЁїABCгыRtЁїABDжаЃЌЁЯC=ЁЯD=90ЁуЃЌADгыBCЯрНЛгкЕуEЃЌдђЁЯCAEгыЁЯDBEЕФДѓаЁЙиЯЕЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкRtЁїABCгыRtЁїABDжаЃЌЁЯC=ЁЯD=90ЁуЃЌADгыBCЯрНЛгкЕуEЃЌдђЁЯCAEгыЁЯDBEЕФДѓаЁЙиЯЕЪЧЃЈЁЁЁЁЃЉ| AЃЎ | ЁЯCAEЃОЁЯDBE | BЃЎ | ЁЯCAE=ЁЯDBE | CЃЎ | ЁЯCAEЃМЁЯDBE | DЃЎ | ЮоЗЈШЗЖЈ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | -50 | BЃЎ | 50 | ||
| CЃЎ | ПЩФмЪЧ+50УзЃЌвВПЩФмЪЧ-50Уз | DЃЎ | вдЩЯЖМВЛЖд |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2.643ЁС103 | BЃЎ | 0.2643ЁС108 | CЃЎ | 26.43ЁС106 | DЃЎ | 2.643ЁС107 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | x2+2$\sqrt{2}$x+1=0 | BЃЎ | x2-2$\sqrt{2}$x-1=0 | CЃЎ | x2-2$\sqrt{2}$x+1=0 | DЃЎ | x2+2$\sqrt{2}$x-1=0 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
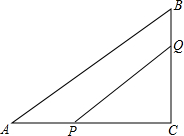 ШчЭМЃЌЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10cmЃЌAC=8cmЃЌЕуPДгAЕуГіЗЂЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгBЕуГіЗЂЯђЕуCвд1cm/sЕФЫйЖШвЦЖЏЃЌЕБЦфжавЛЕуЪзЯШЕНДяжеЕуЪБдЫЖЏЭЃжЙЃЌШєPЁЂQЗжБ№ЭЌЪБДгAЃЌBГіЗЂЃЌМИУыКѓЫФБпаЮAPQBЪЧЁїABCУцЛ§ЕФ$\frac{2}{3}$ЃП
ШчЭМЃЌЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10cmЃЌAC=8cmЃЌЕуPДгAЕуГіЗЂЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгBЕуГіЗЂЯђЕуCвд1cm/sЕФЫйЖШвЦЖЏЃЌЕБЦфжавЛЕуЪзЯШЕНДяжеЕуЪБдЫЖЏЭЃжЙЃЌШєPЁЂQЗжБ№ЭЌЪБДгAЃЌBГіЗЂЃЌМИУыКѓЫФБпаЮAPQBЪЧЁїABCУцЛ§ЕФ$\frac{2}{3}$ЃПВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com