练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．一个等腰三角形的两条边长分别3和6，则该等腰三角形的周长是（　　）
    A．12B．13C．15D．12或15

    分析 分5是腰长与底边长两种情况讨论，由三角形的三边关系和三角形的周长求解即可．

    解答 解：①5是腰长时，三角形的三边分别为3、3、6，
    ∵3+3=6，
    ∴此时不能组成三角形；
    ②3是底边长时，三角形的三边分别为3、6、6，
    此时能组成三角形，
    所以，周长=3+6+6=15．
    综上所述，这个等腰三角形的周长是15，
    故选C．

    点评 本题考查了等腰三角形的性质、三角形的三边关系、三角形周长的计算；熟练掌握等腰三角形的性质，分情况讨论是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．人体中红细胞的直径约为0.0000077m，将数0.0000077用科学记数法表示为（　　）
    A．77×10-5B．0.77×10-7C．7.7×10-6D．7.7×10-7

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若EF=2，BC=10，则AB的长为6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

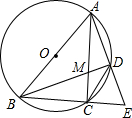    1．如图，△ABC内接于⊙O，AB是⊙O的直径，点D是劣弧AC上的一点，连结AD并延长与BC的延长线交于点E，AC、BD相交于点M．
    （1）求证：BC•CE=AC•MC；
    （2）若点D是劣弧AC的中点，tan∠ACD=$\frac{1}{3}$，MD•BD=10，求⊙O的半径．
    （3）若CD∥AB，过点A作AF∥BC，交CD的延长线于点F，求$\frac{CF}{CD}$-$\frac{BC}{CE}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．若点A（m，y1），B（m+1，y2）都在二次函数y=ax2+4ax+2（a＞0）的图象上，且y1＜y2，则m的取值范围是（　　）
    A．m＞-$\frac{5}{2}$B．m≥-2C．m＜-1D．m≤-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图所示，将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD，再将它绕着中心O顺时针旋转，使其中两个顶点分别与点A和点F重合，得到矩形AMFN，再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上，得到矩形GHIJ，当$\frac{AD}{AB}$=$\frac{5}{6}$时，矩形ABCD的长AB=15；宽AD=18．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

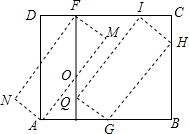    5．如图所示，将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD，再将它绕着中心O顺时针旋转，使其中两个顶点分别与点A和点F重合，得到矩形AMFN，再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上，得到矩形GHIJ，当$\frac{AD}{AB}$=$\frac{5}{6}$时，矩形ABCD的周长为66．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．“中国梦”关乎每个人的幸福生活，为进一步感知我们身边的幸福，展现黄冈人追梦的风采，我市小河中学开展了以“梦想中国，逐梦黄冈”为主题的演讲大赛．为确定演讲顺序，在一个不透明的盒子中放有三张卡片，每张卡片上写有一个实数，分别为3，$\sqrt{2}$，$\sqrt{2}$+6．（卡片除了实数不同外，其余均相同），每组三位参赛学生以抽取的实数大小来决定先后顺序．
    （1）从盒子中随机抽取一张卡片，请直接写出卡片上的实数是3的概率；
    （2）先从盒子中随机抽取一张卡片，将卡片上的实数作为被减数；卡片不放回，再随机抽取一张卡片，将卡片上的实数作为减数，请你用列表法或树状图（树形图）法，求出两次抽取的卡片上的实数之差为有理数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．计算：$\sqrt{2}×\sqrt{4}$=2$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案