
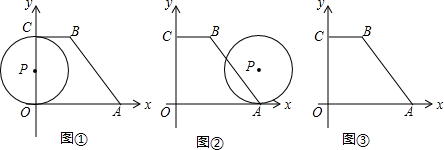
分析 (1)作BD⊥OA于点D,由题意可得BD=OC,要求⊙P的直径,只要求出BD的长即可,根据题目中的数量关系,由勾股定理可以得到BD的长,本题得以解决;
(2)根据题意,画出相应的图形,作AE⊥CP交CB的延长线于点E,根据直径所对的圆周角是直角和勾股定理可以得到AD的长,本题得以解决;
(3)根据题意可知,分两种情况,分别画出相应的图形,然后根据题目中的数量关系和切线的性质,可以分别求得圆心P移动的距离,本题得以解决.
解答 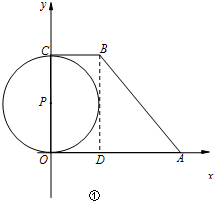 解:(1)如右图①,过B作BD⊥OA.
解:(1)如右图①,过B作BD⊥OA.
由题意知:∠BCO=∠DOC=∠BDO=90°.
∴四边形ODBC为矩形.
∴OC=BD,OD=BC.
∵BC=2,
∴DA=OA-OD=5-2.
在Rt△ABD中,根据勾股定理,得
BD2=AB2-DA2,
∴BD=4,
∴CD=4,
即⊙P的直径是4cm;
(2)如右图②所示,当⊙P与x轴相切于A时,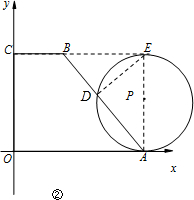
设⊙P与CB所在直线相切于E.
易知P在EA上,且CE=AO=5
∴BE=3
连接ED,
∵EA为直径,
∴∠EDA=90°.
设AD=x,则BD=5-x
由勾股定理知32-(5-x)2=42-x2
解得x=$\frac{16}{5}$
∴AD=$\frac{16}{5}$cm.
(3)如右图③所示,当⊙P与AB相切时,分两种情况.
?第一种情况:当⊙P滚动到P1时,设PP1=x,由题意易知:PP1=CE=OG=x,
则BE=BC-CE=2-x,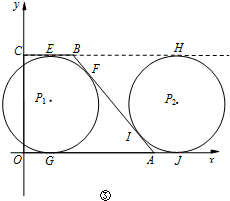 AG=AO-OG=5-x.
AG=AO-OG=5-x.
∵⊙P1与AB、AO相切于点F、G,
∴AF=AG=5-x.
∵⊙P1与BC、AB相切于点E、F,
∴BF=BE=2-x.
∵AB=5,AF+BF=AB,
∴5-x+2-x=5.
解得,x=1,
即PP1=1cm;
第二种情况:?当⊙P滚动到P2时,设PP2=x,易知:OJ=CH=PP2=x,
则AJ=x-5,BH=x-2,
∵⊙P2与AB、CH相切,
∴BI=BH=x-2.
同理,AI=AJ=x-5.
∵AB=BI+AI,
∴x-2+x-5=5.
解得,x=6,
即PP2=6cm;
∴当⊙P与直线AB相切时,点P移动的距离为1cm或6cm.
点评 本题考查圆的综合题、直径所对的圆周角是直角、勾股定理、切线的性质,解题的关键是明确题意,根据题意可以画出相应的图形,作出合适的辅助线,找出所求问题需要的条件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 过点A(1,2)的直线与双曲线y=$\frac{2}{x}$在第一象限内交于点P,直线AO交双曲线的另一分支于点B,且点C(2,1).
过点A(1,2)的直线与双曲线y=$\frac{2}{x}$在第一象限内交于点P,直线AO交双曲线的另一分支于点B,且点C(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4、5、6 | B. | 1、$\sqrt{2}$、$\sqrt{3}$ | C. | 9、40、41 | D. | 1.5、2、2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-2,1) | C. | (2,-1) | D. | (2,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com