
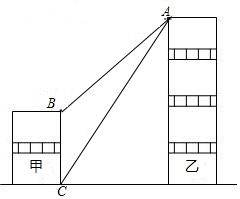
 小颖站在自家阳台的A处用测角仪观察对面的商场,如图,在A处测得商场楼顶B点的俯角为45°,商场楼底C点的俯角为60°,若商场高17.6米,小颖家所在楼房每层楼的平均高度为3米,则小颖家住在几楼?小颖家与商场相距多少米?(结果保留整数,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
小颖站在自家阳台的A处用测角仪观察对面的商场,如图,在A处测得商场楼顶B点的俯角为45°,商场楼底C点的俯角为60°,若商场高17.6米,小颖家所在楼房每层楼的平均高度为3米,则小颖家住在几楼?小颖家与商场相距多少米?(结果保留整数,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414) 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com