
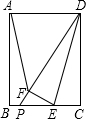
 如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$.
如图,在矩形ABCD中,AB=6,BC=4,点E是边BC上一动点,把△DCE沿DE折叠得△DFE,射线DF交直线CB于点P,当△AFD为等腰三角形时,DP的长为$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$. 分析 先根据AD=BC=4,DF=CD=AB=6,得出AD<DF,再分两种情况进行讨论:①当FA=FD时,过F作GH⊥AD与G,交BC于H,根据△DGF∽△PHF,得出$\frac{PF}{DF}$=$\frac{HF}{GF}$,即$\frac{PF}{6}$=$\frac{6-4\sqrt{2}}{4\sqrt{2}}$,进而解得PF=$\frac{9}{2}$$\sqrt{2}$-6,进而得出DP的长;②当AF=AD=4时,过F作FH⊥BC于H,交DA的延长线于G,根据勾股定理求得FG=$\frac{3}{2}\sqrt{7}$,FH=6-$\frac{3}{2}\sqrt{7}$,再根据△DFG∽△PFH,得出$\frac{PF}{DF}$=$\frac{HF}{GF}$,即$\frac{PF}{6}$=$\frac{6-\frac{3}{2}\sqrt{7}}{\frac{3}{2}\sqrt{7}}$,进而解得PF=$\frac{24}{7}\sqrt{7}$-6,即可得出PD的长.
解答  解:∵AD=BC=4,DF=CD=AB=6,
解:∵AD=BC=4,DF=CD=AB=6,
∴AD<DF,
故分两种情况:
①如图所示,当FA=FD时,过F作GH⊥AD与G,交BC于H,则HG⊥BC,DG=$\frac{1}{2}$AD=2,
∴Rt△DFG中,GF=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$,
∴FH=6-4$\sqrt{2}$,
∵DG∥PH,
∴△DGF∽△PHF,
∴$\frac{PF}{DF}$=$\frac{HF}{GF}$,即$\frac{PF}{6}$=$\frac{6-4\sqrt{2}}{4\sqrt{2}}$,
解得PF=$\frac{9}{2}$$\sqrt{2}$-6,
∴DP=DF+PF=6+$\frac{9}{2}$$\sqrt{2}$-6=$\frac{9}{2}$$\sqrt{2}$;
②如图所示,当AF=AD=4时,过F作FH⊥BC于H,交DA的延长线于G,则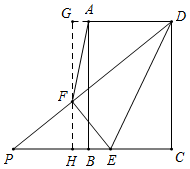
Rt△AFG中,AG2+FG2=AF2,即AG2+FG2=16;
Rt△DFG中,DG2+FG2=DF2,即(AG+4)2+FG2=36;
联立两式,解得FG=$\frac{3}{2}\sqrt{7}$,
∴FH=6-$\frac{3}{2}\sqrt{7}$,
∵∠G=∠FHP=90°,∠DFG=∠PFH,
∴△DFG∽△PFH,
∴$\frac{PF}{DF}$=$\frac{HF}{GF}$,即$\frac{PF}{6}$=$\frac{6-\frac{3}{2}\sqrt{7}}{\frac{3}{2}\sqrt{7}}$,
解得PF=$\frac{24}{7}\sqrt{7}$-6,
∴DP=DF+PF=6+$\frac{24}{7}\sqrt{7}$-6=$\frac{24}{7}\sqrt{7}$,
故答案为:$\frac{9}{2}$$\sqrt{2}$或$\frac{24}{7}\sqrt{7}$.
点评 本题是折叠问题,主要考查了相似三角形的判定与性质,勾股定理,等腰三角形的性质以及矩形的性质的综合应用,解决问题的关键是作辅助线构造相似三角形以及直角三角形,运用相似三角形的对应边成比例列出方程,求得线段的长.解题时注意分类思想的运用.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com