
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
(1)连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由
(2)若BD=![]() CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
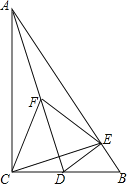
【答案】(1)△CEF是等边三角形.(2)n=60°或135°
【解析】
(1)根据直角三角形斜边的中线等于斜边的一半证得FC=FE即可,再证明∠CFE=60°,从而进行判断;
(2)根据∠B=60°,∠DEB=90°,可知BD=![]() DE,又BD=
DE,又BD=![]() CD,则DC=DE,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,∠CDE等于旋转角,∠CDE=180°-∠BDE=180°-30°=150°.
CD,则DC=DE,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,∠CDE等于旋转角,∠CDE=180°-∠BDE=180°-30°=150°.
(1)∵∠ACB=90°,F是AD中点,
∴FC=![]() AD,
AD,
∵DE⊥AB,F是AD中点,
∴EF=![]() AD,
AD,
∴FC=FE,
∴△CEF是等腰三角形;
又EF=AF,CF=AF,故∠CFE=2∠CAB=60°
从而可知:△CEF是等边三角形.
(2)n=60°或135°
理由:①将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边AC上时,此时记为B'点,如图,
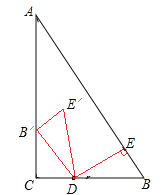
△B'CD为直角三角形,
又∵BD=![]() CD,
CD,
故∠B'DC=45°;从而旋转角∠BDB'=180°-∠B'DC=180°-45°=135°
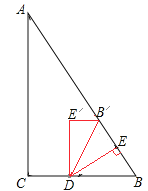
②当B'在边AB上时,有DB=DB',又∠B=60°,故可知△DBB'为等边三角形,所以∠BDB'=60°,即n=60°.
如图,


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
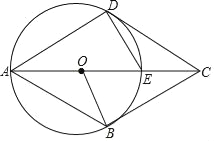
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表三行数的规律,回答下列问题:
第 | 第 | 第 | 第 | 第 | 第 | ... | |
第 |
|
|
|
|
|
| ... |
第 |
|
|
|
|
|
| ... |
第 |
|
|
|
|
|
| ... |
(1)第![]() 行的第四列数
行的第四列数![]() ______________,第
______________,第![]() 行的第六列数
行的第六列数![]() ______________;
______________;
(2)若第![]() 行的某一列的数为
行的某一列的数为![]() ,则第
,则第![]() 的式子表示);
的式子表示);
(3)已知第![]() 列的三个数的和为
列的三个数的和为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在边AB上,且AD=3,DB=2,过点D作DE∥BC,交边AC于点E,将△ADE沿着DE折叠,得△MDE,与边BC分别交于点F,G.若△ABC的面积为15,则△MFG的面积是( )
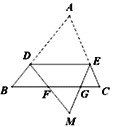
A. 0.5B. 0.6C. 0.8D. 1.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在边AB上(不与点A,B重合),连接DG,作CE⊥DG于点E,AF⊥DG于点F,连接AE,CF.
(1)求证:DE=AF;
(2)若![]() 设
设![]() ,求
,求![]() 的值.
的值.
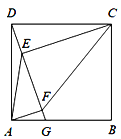
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN的长是______.
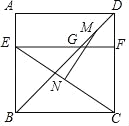
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() -1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
-1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
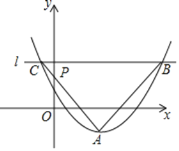
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com