
分析 根据负整数指数幂的意义可得(1$\frac{24}{25}$)${\;}^{-\frac{1}{2}}$=${(\frac{25}{49})}^{\frac{1}{2}}$,再根据分数指数幂的意义得出${(\frac{25}{49})}^{\frac{1}{2}}$-($\frac{1}{27}$)${\;}^{\frac{1}{3}}$=$\frac{5}{7}$-$\frac{1}{3}$,然后计算即可.
解答 解:原式=${(\frac{25}{49})}^{\frac{1}{2}}$-($\frac{1}{27}$)${\;}^{\frac{1}{3}}$
=$\frac{5}{7}$-$\frac{1}{3}$
=$\frac{8}{21}$.
点评 本题考查了负整数指数幂、分数指数幂的意义以及分数的加减运算,掌握定义是解题的关键.


科目:初中数学 来源: 题型:解答题
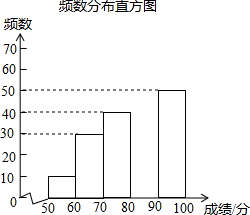 为了传承优秀传统文化,我县团委组织了一次全县有3000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
为了传承优秀传统文化,我县团委组织了一次全县有3000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com