
【题目】某公司生产的商品的市场指导价为每件150元,公司的实际销售价格可以浮动![]() 个百分点[即销售价格
个百分点[即销售价格![]() ],经过市场调研发现,这种商品的日销售量
],经过市场调研发现,这种商品的日销售量![]() (件)与销售价格浮动的百分点
(件)与销售价格浮动的百分点![]() 之间的函数关系如下:
之间的函数关系如下:
浮动 | 0 | 1 | 2 | 3 | … |
销售量 | 24 | 22 | 20 | 18 | … |
若该公司按浮动![]() 个百分点的价格出售,每件商品仍可获利10%.
个百分点的价格出售,每件商品仍可获利10%.
(1)求该公司生产每件商品的成本为多少元?
(2)当实际销售价格定为多少元时,日销售利润为660元?[说明:日销售利润![]() (销售价格
(销售价格![]() 成本)
成本)![]() 日销售量];
日销售量];
(3)该公司决定每销售一件商品就捐赠![]() 元利润(
元利润(![]() )给希望工程,公司通过销售记录发现,当价格浮动的百分点大于
)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于![]() 时,扣除捐赠后的日销售利润随
时,扣除捐赠后的日销售利润随![]() 的增大而减小,直接写出
的增大而减小,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)120元 (2)135元或153元 (3)![]()
【解析】
(1)设该公司生产每件商品的成本为![]() 元,根据“该公司按浮动
元,根据“该公司按浮动![]() 个百分点的价格出售,每件商品仍可获利10%”,列出方程,即可求解;
个百分点的价格出售,每件商品仍可获利10%”,列出方程,即可求解;
(2)先求出![]() 与
与![]() 之间的关系式,再根据“日销售利润
之间的关系式,再根据“日销售利润![]() (销售价格
(销售价格![]() 成本)
成本)![]() 日销售量”,列出方程,即可求解;
日销售量”,列出方程,即可求解;
(3)设日销售利润为W元,先列出W关于x的二次函数解析式,得到二次函数图象的对称轴方程,结合条件,得到关于a的不等式,即可得到答案.
(1)设该公司生产每件商品的成本为![]() 元,依题意得:
元,依题意得:
![]() ,
,
解得:![]() .
.
答:该公司生产每件商品的成本为120元;
(2)设![]() 与
与![]() 之间的关系式为:
之间的关系式为:![]() .
.
当![]() 时,
时,![]() ,
,
则![]() .解得:
.解得:![]() ,
,
∴![]() 与
与![]() 之间的关系式为:
之间的关系式为:![]() .
.
由题意得:![]() ,
,
解得:![]() ,
,![]() .
.
![]() ,
,![]() ,
,
答:商品定价为每件135元或153元,日销售利润为660元;
(3)设日销售利润为W元,
根据题意得:![]()
∴抛物线的对称轴为:直线![]() ,开口向下,
,开口向下,
∵当价格浮动的百分点大于![]() 时,扣除捐赠后的日销售利润随
时,扣除捐赠后的日销售利润随![]() 的增大而减小,
的增大而减小,
∴![]() ,解得:
,解得:![]() ,
,
又∵![]() ,
,
∴![]() 的取值范围:
的取值范围:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿DF直线折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM的长为________.
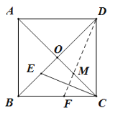
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
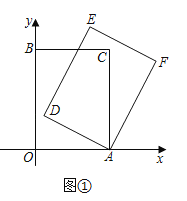
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 △ ABC 中,∠ ACB=90° ,AC=BC=2 .E , F 分别是射线 AC 、CB 上的动点,且 AE=BF , EF 与 AB 交于点 G ,EH⊥ AB 于点 H ,设 AE=x ,GH=y ,下面能够反映 y 与 x 之间函数关系的图象是( )
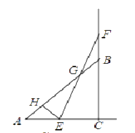
A.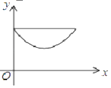 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一服装批发店出售某品牌童装,每件进价120元,批发价200元,多买优惠;凡是一次买10件以上的,每多买一件,所买的全部服装每件就降低1元,但是最低价为为每件160元,
(1)求一次至少买多少件,才能以最低价购买?
(2)写出服装店一次销售x件时,获利润y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲批发了46件,乙批发了50件,店主却发现卖46件赚的钱反而比卖50件赚的钱多,你能用数学知识解释这一现象吗?为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每件160元至少提高到多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分~74分;D级:60分以下)
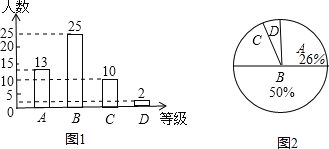
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图(图2)中C级所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OA1B1是等边三角形,点B1的坐标是(2,0),反比例函数y=![]() 的图象经过点A1.
的图象经过点A1.
(1)求反比例函数的解析式.
(2)如图,以B1为顶点作等边三角形B1A2B2,使点B2在x轴上,点A2在反比例函数y=![]() 的图象上.若要使点B2在反比例函数y=
的图象上.若要使点B2在反比例函数y=![]() 的图象上,需将△B1A2B2向上平移多少个单位长度?
的图象上,需将△B1A2B2向上平移多少个单位长度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
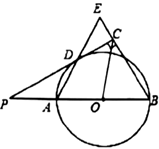
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com