
分析 (1)把A(2,0)代入y=mx2-nx+n-2,即可用含n的代数式表示m;
(2)只需证明△=(-n)2-4m(n-2)>0即可;
(3)①根据题意用含n的代数式表示t,可得t1-t2=$\frac{2{n}_{1}-4}{{n}_{1}+2}$-$\frac{2{n}_{2}-4}{{n}_{2}+2}$=$\frac{8({n}_{1}-{n}_{2})}{({n}_{1}+2)({n}_{2}+2)}$,依此可得t1-t2<0,从而求解;
②t=$\frac{2n-4}{n+2}$=2-$\frac{8}{n+2}$,因为t为整数且n>0,可得n+2>2,得到n+2=4或n+2=8,解方程即可求解.
解答 解:(1)把A(2,0)代入y=mx2-nx+n-2,得4m-2n+n-2=0,m=$\frac{n+2}{4}$;
(2)∵△=(-n)2-4m(n-2)=n2-4×$\frac{n+2}{4}$×(n-2)=n2-n2+4=4>0,
∴二次函数y=mx2-nx+n-2的图象与x轴始终有2个交点;
(3)①依题意可知t=$\frac{2n-4}{n+2}$;
所以t1-t2=$\frac{2{n}_{1}-4}{{n}_{1}+2}$-$\frac{2{n}_{2}-4}{{n}_{2}+2}$=$\frac{8({n}_{1}-{n}_{2})}{({n}_{1}+2)({n}_{2}+2)}$,
因为n1<n2,所以n1-n2<0,
又因为n>0,
所以n1+2>0,n2+2>0,
所以t1-t2<0,
所以t1<t2;
②t=$\frac{2n-4}{n+2}$=2-$\frac{8}{n+2}$,
因为t为整数且n>0,
所以n+2>2,
所以n+2=4或n+2=8
所以n=2或n=6.
点评 本题考查了抛物线与x轴的交点.解答本题的关键是根据根的判别式△>0证明抛物线与x轴有两个交点.


科目:初中数学 来源: 题型:选择题
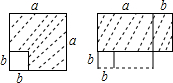 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{16}$的算术平方根是2 | D. | $\sqrt{8}$是最简二次根式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
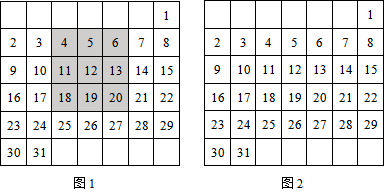
 如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,抛物线m经过点A(-8,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q,则图中阴影部分的面积为32.
如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,抛物线m经过点A(-8,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q,则图中阴影部分的面积为32.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com