已知抛物线的函数关系式为:y=x2+2(a-1)x+a2-2a(a<0),
(1)若点P(-1,8)在此抛物线上.
①求a的值;
②设抛物线的顶点为A,与y轴的交点为B,O为坐标原点,∠ABO=α,求sinα的值;
(2)设此抛物线与x轴交于点C(x1,0)、D(x2,0),x1,x2满足a(x1+x2)+2x1x2<3,且抛物线的对称轴在直线x=2的右侧,求a的取值范围.
分析:(1)①将P点坐标代入抛物线的解析式中即可求出a的值;
②根据抛物线的解析式可求出A、B的坐标,过A作AH⊥y轴于H,则∠ABO=∠ABH=α,在Rt△ABH中,根据A、B的坐标,可求出AH、BH的长,即可求出α的正切值;
(2)求a的取值范围,可从两方面考虑:
①由于C、D是抛物线与x轴的交点,根据韦达定理即可得到x1+x2及x1x2的表达式,然后代值求解,即可得到a的取值范围;
②由于抛物线的对称轴在直线x=2的右侧,那么对称轴x=-(a-1)>2,由此可求出另一个a的取值范围;
联立上述两种情况,即可求得a的取值范围.
解答: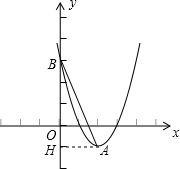
解:(1)①由题设:1-2(a-1)+a
2-2a=8,
解得:a=-1或a=5(舍去).
②y=x
2-4x+3=(x-2)
2-1,
∴A(2,-1),B(0,3).
过A作y轴的垂线,垂足为H,则∠ABO=∠ABH=α.
在Rt△AHB中,AH=2,BH=4,
∴AB=2
,sinα=
=
;
(2)由题设x
1,x
2是方程x
2+2(a-1)x+a
2-2a=0的两根,
∴
∵a(x
1+x
2)+2x
1x
2<3,
∴2a(1-a)+2(a
2-2a)<3,解得a>-
;
又抛物线的对称轴方程是x=1-a,
∴1-a>2,
即a<-1.
综上所述:a的取值范围是-
<a<-1.
点评:此题主要考查了二次函数解析式的确定、锐角三角形函数的定义、根与系数的关系等知识的综合应用能力.

 解:(1)①由题设:1-2(a-1)+a2-2a=8,
解:(1)①由题设:1-2(a-1)+a2-2a=8,

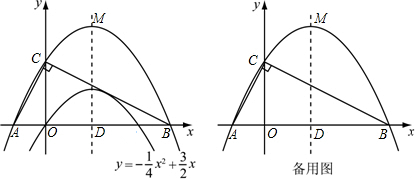
 且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,
且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,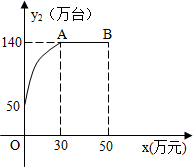 (万元)的关系可用如图所示的抛物线和线段AB表示.其中A为抛物线的顶点.
(万元)的关系可用如图所示的抛物线和线段AB表示.其中A为抛物线的顶点.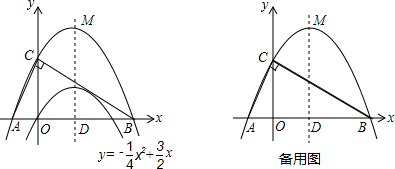
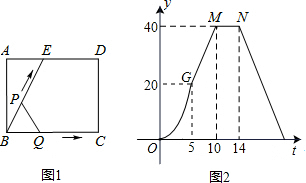 (2013•杭州一模)如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图;
(2013•杭州一模)如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图;