
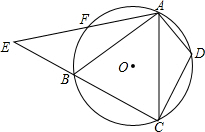
 如图,△ABC内接于⊙O,D,F分别是$\widehat{AC}$与$\widehat{AB}$上的点,$\widehat{BF}$=$\widehat{DA}$,连接AF并延长交CB的延长线于点E,连接AD,CD,求证:△CDA∽△ABE.
如图,△ABC内接于⊙O,D,F分别是$\widehat{AC}$与$\widehat{AB}$上的点,$\widehat{BF}$=$\widehat{DA}$,连接AF并延长交CB的延长线于点E,连接AD,CD,求证:△CDA∽△ABE.  口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
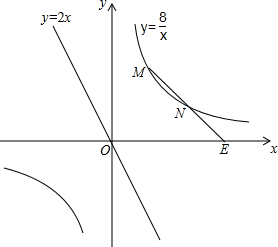 某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.
某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图.
已知:如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y是x的二次函数 | B. | 二次项系数是-10 | C. | 一次项是100 | D. | 常数项是20000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
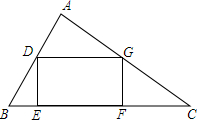 如图,已知△ABC中,BC=24,在△ABC中截出一个矩形DEFG,已知矩形的面积S与EF的长x满足关系式:S=-$\frac{2}{3}$x2+16x,问:EF的长为多少时,矩形的面积等于72?
如图,已知△ABC中,BC=24,在△ABC中截出一个矩形DEFG,已知矩形的面积S与EF的长x满足关系式:S=-$\frac{2}{3}$x2+16x,问:EF的长为多少时,矩形的面积等于72?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com