
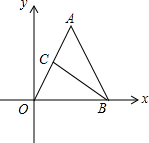
 ��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��A�ڵ�һ���ޣ���B��x���������ϣ�AO=AB��OB=4��tan��AOB=2����C���߶�OA���е㣮
��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��A�ڵ�һ���ޣ���B��x���������ϣ�AO=AB��OB=4��tan��AOB=2����C���߶�OA���е㣮���� ��1������A��AD��OB�ڵ�D������C��CE��OB�ڵ�E����ΪAO=AB�����Ե�D��OB���е㣬����tan��AOB=2�����AD�ij��ȣ�����C��AO���е㣬����CD�ǡ�AOD����λ�ߣ�������λ�ߵ����ʼ������CE�ij��ȣ�
��2�����ڡ�APO=��CBO�������ɣ�1����֪��tan��APO=tan��CBO=$\frac{2}{3}$���Ӷ���֪PD=6����P��x��0������֪|x-2|=6�����x��ֵ�����ô���ϵ����������������ߵĽ���ʽ��
��3������MAD�ס�AOB�����MAN=��AOB�����ڣ�2�����������������߽���ʽ�����Է�����������ۣ������е�N�IJ�ȷ���ԣ����Ե�N��λ�������֣�һ���ǵ�N�ڵ�A���Ϸ�����һ���ǵ�N�ڵ�A���·���
��� �⣺��1������A��AD��OB�ڵ�D��
����C��CE��OB�ڵ�E��
��AO=AB��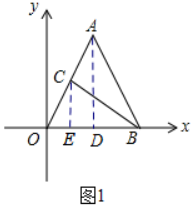
��AD�ǡ�AOB�����ߣ�
��OD=$\frac{1}{2}$OB=2��
��tan��AOB=2��
��$\frac{AD}{OD}=2$��
��AD=4��
��CE��AD��
��C��AO���е㣬
��CE�ǡ�AOD����λ�ߣ�
��CE=$\frac{1}{2}$AD=2��OE=$\frac{1}{2}$OD=1��
��C��������1��2����
��2���ɣ�1����֪��CE=2��BE=3��
A��������2��4����
��tan��CBE=$\frac{CE}{BE}$=$\frac{2}{3}$��
�ߡ�APO=��CBO��
��tan��APO=tan��CBO=$\frac{2}{3}$��
��$\frac{AD}{PD}=\frac{2}{3}$
��PD=6��
��P��������x��0����
��D��2��0����
��PD=|x-2|
��|x-2|=6��
��x=8��x=-4��
��P��8��0����-4��0����
��P������Ϊ��8��0��ʱ��
��A��2��4���ͣ�8��0������y=ax2+bx��
��$\left\{\begin{array}{l}{4=4a+b}\\{0=64a+8b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=\frac{8}{3}}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-$\frac{1}{3}$x2+$\frac{8}{3}$x��
��P������Ϊ��-4��0��ʱ��
��A��2��4����P��-4��0������y=ax2+bx��
��$\left\{\begin{array}{l}{4=4a+2b}\\{0=16a-4b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=\frac{4}{3}}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=$\frac{1}{3}$x2+$\frac{4}{3}$x��
���������������ߵĽ���ʽΪ��y=-$\frac{1}{3}$x2+$\frac{8}{3}$x��y=$\frac{1}{3}$x2+$\frac{4}{3}$x��
��3������MAD�ס�AOBʱ��
�ߡ�AOB�ǵ��������Σ�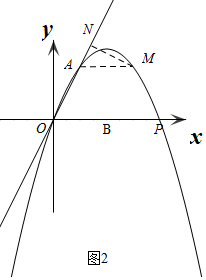
���MAD=��AOB��
�������ߵĽ���ʽΪy=-$\frac{1}{3}$x2+$\frac{8}{3}$xʱ����ͼ2��
����N��A���Ϸ�ʱ��
��ʱ��MAN=��AOB��
��AM��x�ᣬ
��M��������Ϊ4��
���y=4����y=-$\frac{1}{3}$x2+$\frac{8}{3}$x��
��ã�x=2����ȥ����x=6��
��M��������6��4����
����N�ڵ�A���·�ʱ��
��ֱ��AD�Ľ���ʽΪy=kx��
��A��2��4������y=kx��
��y=2x��
��D��a��2a��
�ߡ�MAD�ס�OAB
���MDA=��AOB
��DM��x�ᣬ
����A��AE��DM�ڵ�E������x���ڵ�F
��DE=2-a��
��tan��MDA=tan��AOB=2��
��AE=2DE=4-2a
���ɹ��ɶ�����֪��AD=$\sqrt{5}$��2-a��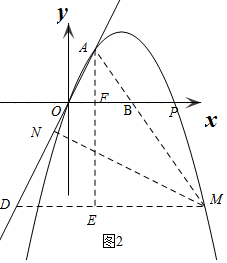
��$\frac{OA}{DM}=\frac{OB}{AD}$
��DM=$\frac{5��2-a��}{4}$
��M�ĺ�����Ϊx��
��x-a=$\frac{5��2-a��}{4}$
��x=$\frac{10-a}{4}$
��M��$\frac{10-a}{4}$��2a��
��M��$\frac{10-a}{4}$��2a������y=-$\frac{1}{3}$x2+$\frac{8}{3}$x��
��2a=-$\frac{1}{3}$��$\frac{10-a}{4}$��2+$\frac{8}{3}$����$\frac{10-a}{4}$��
��ã�a=2��a=-110
�൱a=2ʱ��M��2��4����ȥ
��a=-110ʱ��M��30��-220��
�������ߵĽ���ʽΪy=$\frac{1}{3}$x2+$\frac{4}{3}$xʱ�� ��ͼ3��
��ͼ3��
����N�ڵ�A���Ϸ�ʱ��
��ʱ��MAN=��AOB��
�ӳ�MA��x���ڵ�F��
�ߡ�MAN=��OAF��
���AOB=��OAF��
��FA=FO��
����F��FG��OA�ڵ�G��
��A��2��4����
���ɹ��ɶ�������ã�AO=2$\sqrt{5}$��
��OG=$\frac{1}{2}$AO=$\sqrt{5}$��
��tan��AOB=$\frac{GF}{OG}$
��GF=2$\sqrt{5}$��
���ɹ��ɶ�������ã�OF=5��
��F��������5��0����
��ֱ��MA�Ľ���ʽΪ��y=mx+n��
��A��2��4����F��5��0������y=mx+n��
��$\left\{\begin{array}{l}{4=2k+b}\\{0=5k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=\frac{20}{3}}\end{array}\right.$��
��ֱ��MA�Ľ���ʽΪ��y=-$\frac{4}{3}x$+$\frac{20}{3}$��
����$\left\{\begin{array}{l}{y=\frac{1}{3}{x}^{2}+\frac{4}{3}x}\\{y=-\frac{4}{3}x+\frac{20}{3}}\end{array}\right.$��
���ã�x=2����ȥ����x=-10��
��x=-10����y=-$\frac{4}{3}x$+$\frac{20}{3}$��
��y=20��
��M��-10��20����
����N�ڵ�A���·�ʱ��
��ʱ��MAN=��AOB��
��AM��x�ᣬ
��M��������Ϊ4��
��y=4����y=$\frac{1}{3}$x2+$\frac{4}{3}$x��
��x=-6��x=2����ȥ����
��M��-6��4����
�������������������ĵ�M��6��4����-10��20����-6��4����30��-220����ʹ�á�MAD�ס�AOB
���� ���⿼����κ������ۺ����⣬�漰���ɶ���������ϵ���������ʽ���ⷽ�̴�ֱƽ���ߵ����ʵ�֪ʶ�����ݽ�Ϊ�ۺϣ���Ҫѧ����������ѧ��֪ʶ���н��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
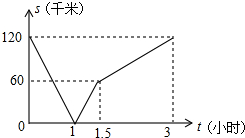 ����Ħ�г���A��ȥB�أ��ҿ�������B��ȥA�أ�ͬʱ������������ʻ�����Ե����յ��ֹͣ����ס������˼����Ϊs����λ�����ף�������ʻ��ʱ��Ϊs����λ��Сʱ����s��t֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ��������ٶȴ���Ħ�г��ٶȣ����ٳ���1Сʱ���ס�����;���������ڳ���1.5Сʱ������ʻ��60ǧ�ף��۳���2Сʱ���ס������8O���ף��ܳ���3Сʱ���ס���ͬʱ����Ŀ�ĵأ����У���ȷ���۵ĸ����ǣ�������
����Ħ�г���A��ȥB�أ��ҿ�������B��ȥA�أ�ͬʱ������������ʻ�����Ե����յ��ֹͣ����ס������˼����Ϊs����λ�����ף�������ʻ��ʱ��Ϊs����λ��Сʱ����s��t֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ��������ٶȴ���Ħ�г��ٶȣ����ٳ���1Сʱ���ס�����;���������ڳ���1.5Сʱ������ʻ��60ǧ�ף��۳���2Сʱ���ס������8O���ף��ܳ���3Сʱ���ס���ͬʱ����Ŀ�ĵأ����У���ȷ���۵ĸ����ǣ�������| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ס�����̨�������ӹ�һ��������ڼӹ���������̨�������ı���һ�ι���Ч�ʣ��ӹ�����ʼ���ӹ������������̨����ǡ��ͬʱ����6Сʱ���ס�����̨�������Լӹ����������y��������ӹ�ʱ��x��ʱ��֮��ĺ���ͼ��ֱ�Ϊ����OA-AB������OC-CD����ͼ��ʾ��
�ס�����̨�������ӹ�һ��������ڼӹ���������̨�������ı���һ�ι���Ч�ʣ��ӹ�����ʼ���ӹ������������̨����ǡ��ͬʱ����6Сʱ���ס�����̨�������Լӹ����������y��������ӹ�ʱ��x��ʱ��֮��ĺ���ͼ��ֱ�Ϊ����OA-AB������OC-CD����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB=10cm����C��D��AB�ϣ���CB=4cm��D��AC���е㣮
��ͼ��AB=10cm����C��D��AB�ϣ���CB=4cm��D��AC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | û��ʵ���� | B�� | ֻ��һ��ʵ���� | ||
| C�� | ��������ȵ�ʵ���� | D�� | ����������ȵ�ʵ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
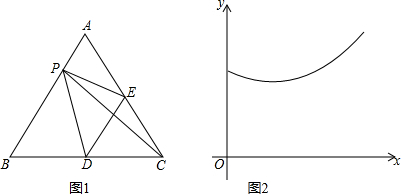
| A�� | �߶�DE | B�� | �߶�PD | C�� | �߶�PC | D�� | �߶�PE |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���BOC�ǵ��������Σ���B��x���������ϣ���OAD�ǡ�OBC�Ƶ�O��ʱ����ת60��õ��ģ���A��y���������ϣ�����DC���߶�OA�ij��ǹ���x�ķ���x2-4x+4=0�ĸ�
��ͼ����ƽ��ֱ������ϵ�У���BOC�ǵ��������Σ���B��x���������ϣ���OAD�ǡ�OBC�Ƶ�O��ʱ����ת60��õ��ģ���A��y���������ϣ�����DC���߶�OA�ij��ǹ���x�ķ���x2-4x+4=0�ĸ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com