
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈ ![]() ,cos67°≈
,cos67°≈ ![]() ,tan67°≈
,tan67°≈ ![]() ,
, ![]() ≈1.73)
≈1.73)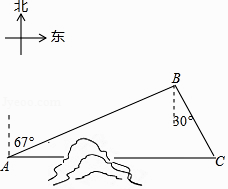
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD. 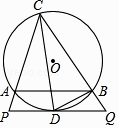
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程x+ ![]() =m的两实根,且tan∠PCD=
=m的两实根,且tan∠PCD= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b(k≠0)的图象经过A(﹣1,﹣4),B(2,2)两点,P为反比例函数y= ![]() 图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )
图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )
A.2
B.4
C.8
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°,如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s,EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连接AF,FQ,当点Q停止运动时,△EFQ也停止运动.设运动时间为t(s)(0<t<6),解答下列问题: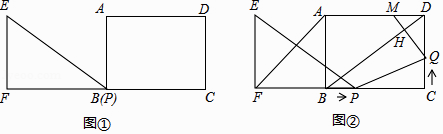
(1)当t为何值时,PQ∥BD?
(2)设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形AFPQM:S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.
(4)在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE. 
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°,CE=2BE,试判断△CDE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com