
【题目】如图:(1)画![]() 的外角
的外角![]() ,再画
,再画![]() 的平分线
的平分线![]() .(尺规作图)
.(尺规作图)
(2)若![]() ,请完成下面的证明:
,请完成下面的证明:
已知:![]() 中,
中,![]() ,
,![]() 是外角
是外角![]() 的平分线.
的平分线.
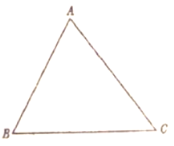
求证:![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知 ![]() ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留 ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.

(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省平遥县政府为进一步挖掘“双林寺、老醯水镇、平遥古城”的旅游 价值,计划在2019年开工建设一条途经平遥高铁站、双林寺、老醯(读![]() ,醋的意思) 水镇、平遥古城的“旅游+交通”融合轨道观光线.甲、乙两个工程队计划参与工程建设,若让甲队单独施工
,醋的意思) 水镇、平遥古城的“旅游+交通”融合轨道观光线.甲、乙两个工程队计划参与工程建设,若让甲队单独施工![]() 天完成该项工程的
天完成该项工程的![]() ,然后乙队加入,两队还需共同施工
,然后乙队加入,两队还需共同施工![]() 天,才能完成该项工程.
天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若先让甲队施工且甲队参与该项工程施工的时间不超过![]() 天,则乙队加入后至 少要施工多少天才能完成该项工程?
天,则乙队加入后至 少要施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形例如:某三角形三边长分别是5,6和8,因为![]() ,所以这个三角形是常态三角形.
,所以这个三角形是常态三角形.
(1)若△ABC三边长分别是2,![]() 和4,则此三角形 常态三角形(填“是”或“不是”);
和4,则此三角形 常态三角形(填“是”或“不是”);
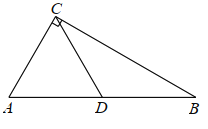
(2)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,CD=![]() AB, 若△ACD是常态三角形,求△ABC的面积;,
AB, 若△ACD是常态三角形,求△ABC的面积;,
(3)若Rt△ABC是常态△,斜边是![]() ,则此三角形的两直角边的和= .
,则此三角形的两直角边的和= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P是边BC上的中点,PD⊥AB,PE⊥AC,垂足分别为点D、E.
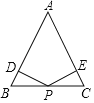
(1)求证:PD=PE;
(2)若AB=6cm,∠BAC=30°,请直接写出PD+PE= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
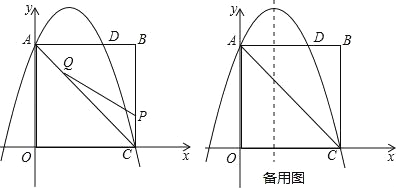
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
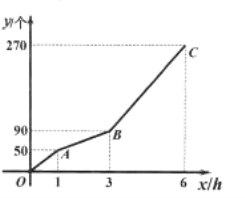
【题目】甲、乙两台机器共同加工一批零件,一共用了![]() 小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数
小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数![]() (个)与甲加工时间
(个)与甲加工时间![]() 之间的函数图象为折线
之间的函数图象为折线![]() ,如图所示.
,如图所示.
(1)这批零件一共有 个,甲机器每小时加工 个零件,乙机器排除故障后每小时加工 个零件;
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(3)在整个加工过程中,甲加工多长时间时,甲与乙加工的零件个数相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com