

分析 (1)由△ADE等腰直角三角形得出AD=$\sqrt{2}$AE=$\sqrt{2}$CE,故$\frac{CE}{AD}$的值为$\frac{\sqrt{2}}{2}$;
(2)证明△AEC≌△DEC,求出∠ACE=22.5°,∠EAC=22.5°,得到AE=CE,在等腰直角三角形△ADE中,AD=$\sqrt{2}$AE,则AD=$\sqrt{2}$CE;
(3)成立,作AF⊥BC,连接EF,易知A、E、D、F四点共圆,则∠EDC=∠EAF,证明△AEF≌△CEF,得出ED=EC,则AD=$\sqrt{2}$CE;
解答 解:(1)∵△ADE等腰直角三角形,
∴AD=$\sqrt{2}$AE,
∵∠BAC=90°,AB=AC,D是BC边中点,
∴AE=CE,
∴AD=$\sqrt{2}$CE,
∴$\frac{CE}{AD}$=$\frac{\sqrt{2}}{2}$;
故答案为:$\frac{\sqrt{2}}{2}$.
(2)AD=$\sqrt{2}$CE;
在△AEC和△DEC中,
$\left\{\begin{array}{l}{CA=CD}\\{AE=DE}\\{CE=CE}\end{array}\right.$,
∴△AEC≌△DEC,
∴∠ACE=∠DCE=$\frac{1}{2}$∠ACD=22.5°,
∵CA=CD,∠ACD=45°,
∴∠CAD=67.5°,
∵∠EAD=45°,
∴∠EAC=22.5°,
∴∠EAC=∠ECA,
∴AE=CE,
∵△ADE等腰直角三角形,
∴AD=$\sqrt{2}$AE,
∴AD=$\sqrt{2}$CE;
(3)成立;
作AF⊥BC,连接EF,
∵∠BAC=90°,AB=AC,
∴AF=CF,
∵∠AFC=∠AED=90°,
∴A、E、D、F四点共圆,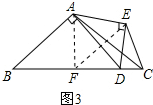
∴∠EDC=∠EAF,
∵AE=DE,
∴∠AFE=∠EFD
在△AFE和△CFE中,
$\left\{\begin{array}{l}{AF=CF}\\{∠AFE=∠EFD}\\{FE=FE}\end{array}\right.$,
∴△AFE≌△CFE,
∴∠FAE=∠FCE,
∴∠EDC=∠ECD,
∴ED=ED,
∵AD=$\sqrt{2}$DE,
∴AD=$\sqrt{2}$CE.
点评 本题主要考查了全等三角形的判定与性质以及等腰直角三角形的判定与性质,熟练掌握全等三角形的判定方法以及等腰直角三角形的性质是解决问题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
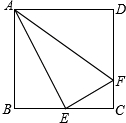 如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.
如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
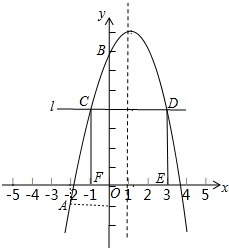 如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.
如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}{-0.05x+0.25(1≤x<4且x为整数)}\\{0.1(4≤x≤6且x为整数)}\\{0.015x+0.01(6<x≤12且x为整数)}\end{array}\right.$,一年后发现实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
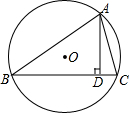 如图,O是△ABC的外心,AD是BC边上的高,R是△ABC外接圆的半径.问:
如图,O是△ABC的外心,AD是BC边上的高,R是△ABC外接圆的半径.问:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,中线BE与中线CD交于点G,若M为BE的中点,N为CD的中点,则$\frac{MN}{DE}$=$\frac{1}{2}$.
如图,在△ABC中,中线BE与中线CD交于点G,若M为BE的中点,N为CD的中点,则$\frac{MN}{DE}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com