
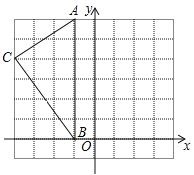
【题目】如图,△ABC在平面直角坐标系的坐标分别为A(﹣1,5),B(﹣1,0),C(﹣4,3),按要求完成:
(1)在同一坐标系中,画出△ABC关于y轴对称的图形△A'B'C';
(2)若CD是△ABC中AB边的中线,E是CD的中点,F是AE的中点,连接AE、BE,FB,则△EFB的面积S= .
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
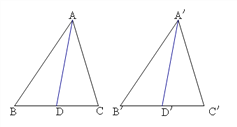
【题目】如图,△ABC≌△A'B'C',AD、A'D'分别是△ABC、△A'B'C'的对应边上的中线,判断AD与A'D'有怎样的数量关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.

(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(x1,y1)、B(x2,y2)都在直线y=kx+2(k<0)上,且x1<x2则y1、y2的大小关系是( )
A.y1 =y2B.y1 <y2C.y1 >y2D.y1 ≥y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
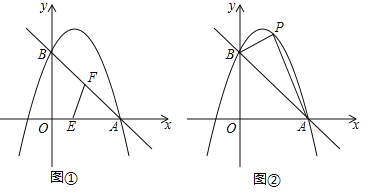
【题目】如图,已知抛物线![]() 经过A(3,0),B(0,3)两点.
经过A(3,0),B(0,3)两点.
(1)求此抛物线的解析式和直线AB的解析式;
(2)如图①,动点E从O点出发,沿着OA方向以1个单位/秒的速度向终点A匀速运动,同时,动点F从A点出发,沿着AB方向以![]() 个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
(3)如图②,取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A,B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标;如果不存在,请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com