
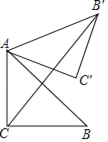
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=![]() ,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为( )
,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为( )
A. ![]() +
+![]() B. 1+
B. 1+![]() C. 3D.
C. 3D. ![]() +
+![]()
科目:初中数学 来源: 题型:
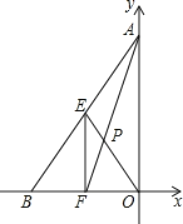
【题目】如图,在平面直角坐标系中,O为坐标原点,点A,B的坐标分别为(0,4),(﹣3,0),E为AB的中点,EF∥AO交OB于点F,AF与EO交于点P,则EP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
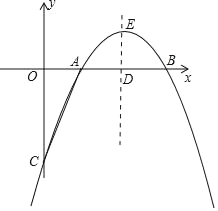
【题目】如图所示,已知抛物线y=﹣x2+bx+c与x轴相交于A、B两点,且点A的坐标为(1,0),与y轴交于点C,对称轴直线x=2与x轴相交于点D,点P是抛物线对称轴上的一个动点,以每秒1个单位长度的速度从抛物线的顶点E向下运动,设点P运动的时间为t(s).
(1)点B的坐标为 ,抛物线的解析式是 ;
(2)求当t为何值时,△PAC的周长最小?
(3)当t为何值时,△PAC是以AC为腰的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行“校园朗读者”朗诵大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
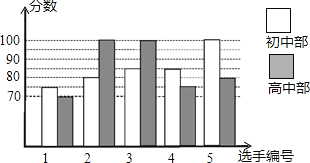
(1)根据图示填写表格;
平均分(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(2)结合两队成绩的平均数和中位数, 队的决赛成绩较好;
(3)已知高中代表队决赛成绩的方差为160,计算初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.(方差公式:S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]
)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x二次函数y=x2﹣(2k+1)x+(k2+5k+9)与x轴有交点.
(1)求k的取值范围;
(2)若x1,x2是关于x的方程x2﹣(2k+1)x+(k2+5k+9)=0的两个实数根,且x12+x22=39,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
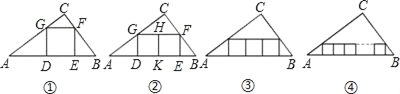
【题目】猜想归纳:为了建设经济型节约型社会,“先锋”材料厂把一批三角形废料重新利用,因此工人师傅需要把它们截成不同大小的正方形铁片.(已知:AC=40,BC=30,∠C=90°)
(1)如图①,若截取△ABC的内接正方形DEFG,请你求出此正方形的边长;
(2)如图②,若在△ABC内并排截取两个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(3)如图③,若在△ABC内并排截取三个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(4)猜想:如图④,假设在△ABC内并排截取n个相同的正方形,使它们组成的矩形内接于△ABC,则此正方形的边长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空自部分面积为10.5,则阴影部分面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com