
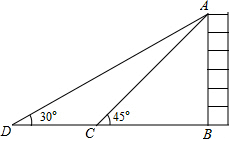
 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.
如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.分析 设AB=x米,由∠ACB=45°得BC=AB=x、BD=BC+CD=x+100,根据tan∠ADB=$\frac{AB}{BD}$可得关于x的方程,解之可得答案.
解答 解:设AB=x米,
在Rt△ABC中,∵∠ACB=45°,
∴BC=AB=x米,
则BD=BC+CD=x+100(米),
在Rt△ABD中,∵∠ADB=30°,
∴tan∠ADB=$\frac{AB}{BD}$=$\frac{\sqrt{3}}{3}$,即$\frac{x}{x+100}$=$\frac{\sqrt{3}}{3}$,
解得:x=50+50$\sqrt{3}$≈137,
即建筑物AB的高度约为137米
故答案为:137.
点评 本题考查解直角三角形的应用-仰角俯角问题,解题的关键是利用数形结合的思想找出各边之间的关系,然后找出所求问题需要的条件.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
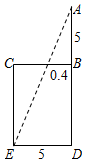 “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )| A. | 1.25尺 | B. | 57.5尺 | C. | 6.25尺 | D. | 56.5尺 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
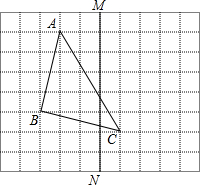 如图,在正方形网格上有一个△ABC.
如图,在正方形网格上有一个△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com