Question

4．已知半径为2的⊙O中，弦AB=2$\sqrt{2}$，则弦AB所对的圆周角∠P=45°或135°．．

Answer 1

分析 连接OA、OB，如图，利用勾股定理的逆定理可证明△OAB直角三角形，∠AOB=90°，再利用圆周角定理得到∠APB=45°，接着根据圆内接四边形的性质得∠AP′B=135°，从而得到弦AB所对的圆周角．

解答 解：连接OA、OB，如图，
∵OA=OB=2，AB=2$\sqrt{2}$，
∴OA²+OB²=AB²，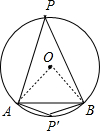
∴△OAB直角三角形，∠AOB=90°，
∴∠APB=$\frac{1}{2}$∠AOB=45°，
∴∠AP′B=180°-∠ACB=135°，
即弦AB所对的圆周角为45°或135°．
故答案为45°或135°．

点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．注意分类讨论的运用．