
【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
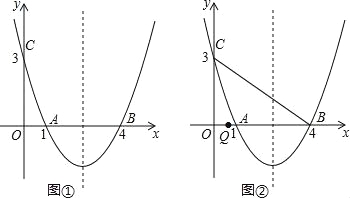
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+3(2)9(3)(
x+3(2)9(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
试题分析:(1)把点A(1,0)、B(4,0)、C(0,3)三点的坐标代入函数解析式,利用待定系数法求解;
(2)A、B关于对称轴对称,连接BC,则BC与对称轴的交点即为所求的点P,此时PA+PC=BC,四边形PAOC的周长最小值为:OC+OA+BC;根据勾股定理求得BC,即可求得;
(3)分两种情况分别讨论,即可求得.
试题解析:(1)根据题意设抛物线的解析式为y=a(x﹣1)(x﹣4),
代入C(0,3)得3=4a,
解得a=![]() ,
,
y=![]() (x﹣1)(x﹣4)=
(x﹣1)(x﹣4)=![]() x2﹣
x2﹣![]() x+3,
x+3,
所以,抛物线的解析式为y=![]() x2﹣
x2﹣![]() x+3.
x+3.
(2)∵A、B关于对称轴对称,如图1,连接BC,
∴BC与对称轴的交点即为所求的点P,此时PA+PC=BC,
∴四边形PAOC的周长最小值为:OC+OA+BC,
∵A(1,0)、B(4,0)、C(0,3),
∴OA=1,OC=3,BC=![]() =5,
=5,
∴OC+OA+BC=1+3+5=9;
∴在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9.
(3)∵B(4,0)、C(0,3),
∴直线BC的解析式为y=﹣![]() x+3,
x+3,
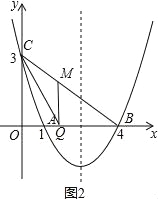
①当∠BQM=90°时,如图2,设M(a,b),
∵∠CMQ>90°,
∴只能CM=MQ=b,
∵MQ∥y轴,
∴△MQB∽△COB,
∴![]() ,
,
即![]() ,解得b=
,解得b=![]() ,代入y=﹣
,代入y=﹣![]() x+3得,
x+3得,![]() =﹣
=﹣![]() a+3,解得a=
a+3,解得a=![]() ,
,
∴M(![]() ,
,![]() );
);
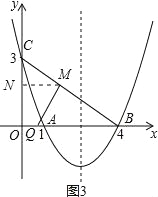
②当∠QMB=90°时,如图3,
∵∠CMQ=90°,
∴只能CM=MQ,
设CM=MQ=m,
∴BM=5﹣m,
∵∠BMQ=∠COB=90°,∠MBQ=∠OBC,
∴△BMQ∽△BOC,
∴![]() ,解得m=
,解得m=![]() ,
,
作MN∥OB,
∴![]() ,即
,即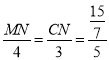
∴MN=![]() ,CN=
,CN=![]() ,
,
∴ON=OC﹣CN=3﹣![]() =
=![]() ,
,
∴M(![]() ,
,![]() ),
),
综上,在线段BC上存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形,点M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】长方形的一边长等于3m+2n,其邻边长比它长m-n,则这个长方形的周长是( )
A. 14m+6n B. 7m+3n
C. 4m+n D. 8m+2n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是______________.(填序号)
;④0<CE≤6.4.其中正确的结论是______________.(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
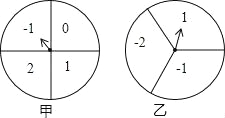
【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣![]() x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣![]() x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣![]() x+3于点Q,则当PQ=BQ时,a的值是 .
x+3于点Q,则当PQ=BQ时,a的值是 .
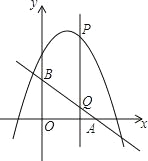
查看答案和解析>>
科目:初中数学 来源: 题型:
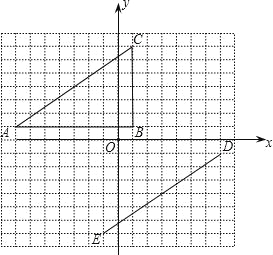
【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,﹣1),E(﹣1,﹣7).
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数. 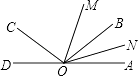
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库.
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com