
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象
)的图象![]() 经过点
经过点![]() (4,1),直线
(4,1),直线![]() 与图象
与图象![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 在点
在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内恰有4个整点,结合函数图象,求
内恰有4个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
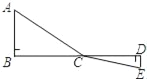
【题目】阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为![]() .然后利用几何知识可知:当A、C、E在一条直线上时,x=
.然后利用几何知识可知:当A、C、E在一条直线上时,x=![]() 时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式
时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式![]() 的最小值为_____.
的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
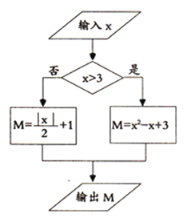
【题目】嘉淇设计了一个如图所示的数值转换程序.
(1)当输入![]() 时,输出
时,输出![]() 的值为 .当输入
的值为 .当输入![]() 时,输出
时,输出![]() 的值为 ;
的值为 ;
(2)若(1)中![]() 的两个数值依次对应数轴上的点
的两个数值依次对应数轴上的点![]() ,
,![]() ,点
,点![]() 为数轴上另外一点,且满足
为数轴上另外一点,且满足![]() ,求点
,求点![]() 对应的数;
对应的数;
(3)当输出![]() 的值为15时,求输入
的值为15时,求输入![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若![]() .
.
①求抛物线的解析式;
②当线段PD的长度最大时,求点P的坐标;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
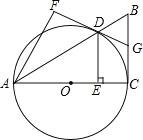
【题目】如图,已知Rt△ABC中,∠ACB=90°,以AC为直径的圆O交斜边AB于D.过D作DE⊥AC于E,将△ADE沿直线AB翻折得到△ADF.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为10,sin∠FAD=![]() ,延长FD交BC于G,求BG的长.
,延长FD交BC于G,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两列火车分别从![]() ,
,![]() 两城同时匀速驶出,甲车开往
两城同时匀速驶出,甲车开往![]() 城,乙车开往
城,乙车开往![]() 城.由于墨迹遮盖,图中提供的只是两车距
城.由于墨迹遮盖,图中提供的只是两车距![]() 城的路程
城的路程![]() (千米),
(千米),![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)的函数图象的一部分.
(时)的函数图象的一部分.
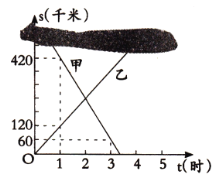
(1)乙车的速度为_______________千米![]() 时;
时;
(2)分别求出![]() ,
,![]() 与
与![]() 的函数解析式(不必写出
的函数解析式(不必写出![]() 的取值范围);
的取值范围);
(3)求出两城之间的路程,及![]() 为何值时两车相遇;
为何值时两车相遇;
(4)当两车相距![]() 千米时,求
千米时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com