
【题目】抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1,0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是( )
A.方程ax2+bx+c=2的一个根是x=﹣2
B.若x1=2,则抛物线与x轴的另一个交点为(﹣4,0)
C.若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2
D.若![]() ≤x≤0时,2≤y≤3,则a=
≤x≤0时,2≤y≤3,则a=![]()
【答案】D
【解析】
根据已知条件可将二次函数y=ax2+bx+c变形为y =a(x+1)2﹣a+2,把x=-2代入,可对A进行判断;利用对称性可对B进行判断;依据一元二次方程根的差别式可对C进行判断;根据抛物线的图象与性质可对D进行判断.
解:由已知可得,c=2,b=2a,
∴y=ax2+2ax+2=a(x2+2x)+2=a(x+1)2﹣a+2,
A.当x=﹣2时,y=2,
∴方程ax2+bx+c=2的一个根是x=﹣2;故A正确,不符合题意;
B.若x1=2,函数的对称轴为直线x=﹣1,则抛物线与x轴的另一个交点为(﹣4,0),正确,不符合题意;
C.ax2+2ax+2=4时,△=4a2+8a=0,
∴a=0或a=﹣2,
∴a=﹣2,正确,不符合题意;
D.若﹣![]() ≤x≤0时2≤y≤3;
≤x≤0时2≤y≤3;
在﹣![]() ≤x≤0时,当x=﹣1时,y有最大值2﹣a,当x=0时,有最最小值2;
≤x≤0时,当x=﹣1时,y有最大值2﹣a,当x=0时,有最最小值2;
∴3=2﹣a,
∴a=﹣1,
故D.错误,符合题意;
故选:D.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
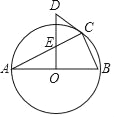
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
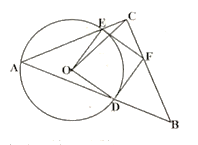
【题目】如图,等腰![]() 的一个锐角顶点
的一个锐角顶点![]() 是
是![]() 上的一个动点,
上的一个动点,![]() ,腰
,腰![]() 与斜边
与斜边![]() 分别交
分别交![]() 于点
于点![]() ,分别过点
,分别过点![]() 作
作![]() 的切线交于点
的切线交于点![]() ,且点
,且点![]() 恰好是腰
恰好是腰![]() 上的点,连接
上的点,连接![]() ,若
,若![]() 的半径为4,则
的半径为4,则![]() 的最大值为:( )
的最大值为:( )
A.![]() B.
B.![]() C.6D.8
C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
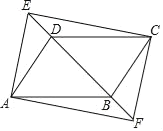
【题目】如图,在ABCD中,点E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AFCE是平行四边形.
(2)若BD⊥AD,AB=5,AD=3,四边形AFCE是矩形,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
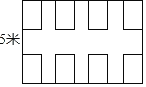
【题目】如图所示的是一个宽5米的餐厅,只能放8张餐桌.现计划扩建增加座位,只能对原宽度进行加长,设加长后的长度为m米.若餐厅的餐桌数为y,经计算,得到如下数据:(注:m和y都为正整数)
m(米) | 5 | 8 | 11 | 14 | …… |
餐桌数y(张) | 8 | 12 | 16 | …… |
(1)根据表中数据的规律,完成以上表格;
(2)求出y关于m的函数解析式;
(3)若这家餐厅至少要有80张餐桌,求m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,请用直尺(不带刻度),和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMNP,使点M,N、P在边AB、BC、CA上;
(2)当∠A=60°,AB=4,AC=3时,求菱形AMNP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司用6000元购进A,B两种电话机25台,购买A种电话机与购买B种电话机的费用相等.已知A种电话机的单价是B种电话机单价的1.5倍.
(1)求A,B两种电话机的单价各是多少?
(2)若计划用不超过8000元的资金再次购进A,B两种话机共30台,已知A,B两种电话机的进价不变,求最多能购进多少台A种电话机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学就“戏曲进校园”活动的喜爱情况进行了随机调查,对收集的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:(图中![]() 表示“很喜欢”,
表示“很喜欢”,![]() 表示“喜欢”,
表示“喜欢”,![]() 表示“一般”,
表示“一般”,![]() 表示“不喜欢”)
表示“不喜欢”)
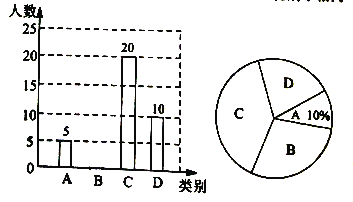
(1)被调查的总人数是_________,扇形统计图中![]() 部分所对应的扇形圆心角的度数为_________;
部分所对应的扇形圆心角的度数为_________;
(2)补全条形统计图;
(3)在抽取的![]() 类5人中,刚好有甲、乙、丙3个女生和丁、戊2个男生,从中随机抽取两个同学担任两角色,用画树状图或列表法求出抽到的两个学生性别不相同的概率.
类5人中,刚好有甲、乙、丙3个女生和丁、戊2个男生,从中随机抽取两个同学担任两角色,用画树状图或列表法求出抽到的两个学生性别不相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com