
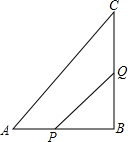
 如图所示的Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1厘米/秒的速度向点A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为35平方厘米?PQ的距离是多少厘米?(结果用最简二次根式表示)
如图所示的Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1厘米/秒的速度向点A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为35平方厘米?PQ的距离是多少厘米?(结果用最简二次根式表示) 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
 22、在如图所示的Rt△ABC的纸片上,∠C=90°,请用尺规作图画出一个正方形CDEF,使点E落在斜边AB上.(不必写作法和证明,请保留作图痕迹)
22、在如图所示的Rt△ABC的纸片上,∠C=90°,请用尺规作图画出一个正方形CDEF,使点E落在斜边AB上.(不必写作法和证明,请保留作图痕迹)查看答案和解析>>
科目:初中数学 来源:2011年贵州省毕节地区中考数学真题试卷(解析版) 题型::选择题
如图所示的Rt△ABC绕直角边AB旋转一周,所得几何体的主视图为( )
 A、
A、 B、
B、
C、 D、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com