练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：(1) ；(2) ；

    (3)；(4)

    【答案】（1）－3；（2）；（3）；（4）

    【解析】

    有理数的加减混合运算，可以利用加法的运算律将负数与正数分开分别相加，这样可以减少异号两数相加易犯的错误，整式加减运算先去括号，然后合并同类项即可.

    解：（1）原式=6—0.5—10＋1.5=（6－10）＋（－0.5＋1.5）=－4＋1=－3；

    （2）原式=－3－＋4 =（－3＋4）－ =1－ =；

    (3)原式== ==；

    (4)原式==.

    “点睛”本题在运算过程中第一步是将加减统一成加法，第二步是省略加号写成代数和的形式，第三步是运用了加法交换律，第四步是运用了加法结合律，后面是利用加法法则，通过运算过程我们还可以看到加法的运算律在运算中的重要作用.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若x=1，y=，则x2+4xy+4y2的值是（ ）

    A. 2 B. 4 C. 32 D. 12

    【答案】B

    【解析】解析：x2+4xy+4y2=（x+2y）2==4.故选B.

    【题型】单选题
    【结束】
    9

    【题目】下列因式分解，正确的是（ ）

    A. x2y2-z2=x2（y+z）（y-z） B. -x2y+4xy-5y=-y（x2+4x+5）

    C. （x+2）2-9=（x+5）（x-1） D. 9-12a+4a2=-（3-2a）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

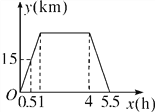
    【题目】周末，小李从家里出发骑车到少年宫学习绘画，学完后立即回家，他离家的距离y(km)与时间x(h)之间的函数关系如图所示，有下列结论：①他家离少年宫30km；②他在少年宫一共停留了3h；③他返回家时，离家的距离y(km)与时间x(h)之间的函数表达式是y＝－20x＋110；④当他离家的距离y＝10时，时间x＝.其中正确的是________(填序号)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在社会主义新农村建设中，衢州某乡镇决定对A、B两村之间的公路进行改造，并有甲工程队从A村向B村方向修筑，乙工程队从B村向A村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务有甲工程队单独完成，直到公路修通．下图是甲乙两个工程队修公路的长度y（米）与施工时间x（天）之间的函数图象，请根据图象所提供的信息解答下列问题：

    （1）乙工程队每天修公路多少米？

    （2）分别求甲、乙工程队修公路的长度y（米）与施工时间x（天）之间的函数关系式．

    （3）若该项工程由甲、乙两工程队一直合作施工，需几天完成？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地A、B两村盛产柑橘，A村有柑橘200吨，B村有柑橘300吨，现将这些柑橘运到C、D两个冷藏仓库．已知C仓库可储存240吨，D仓库可储存260吨，从A村运往C、D两处的费用分别为每吨20元、25元，从B村运往C、D两处的费用分别为每吨15元、18元．设从A村运往C仓库的柑橘重量为x吨，A、B两村运往两仓库的柑橘运输费用分别为yA元、yB元．

    (1)请填写下表，并求出yA、yB与x之间的函数表达式；

    (2)试讨论A、B两村中，哪个村的运费较少；

    (3)考虑到B村的经济承受能力，B村的柑橘运费不得超过4830元，在这种情况下，请问怎样调运才能使两村运费之和最小？求出这个最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：三角形中，、分别是和的平分线，、相交于点（知识链接：三角形三个内角的和是180°。如图是三角形的一个内角）

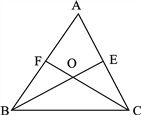
    （1）如果°求的度数。

    （2）如果°直接写出的度数

    （3）探求和的关系（用等式表示），并简要说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为发展校园足球运动，某县城区四校决定联合购买一批足球运动装备，市场调查发现：甲、乙两商场以同样的价格出售同种品牌的足球队服和足球，已知每套队服比每个足球多50元，两套队服与三个足球的费用相等，经洽谈，甲商场优惠方案是：每购买十套队服，送一个足球；乙商场优惠方案是：若购买队服超过80套，则购买足球打八折．

    （1）求每套队服和每个足球的价格是多少？

    （2）若城区四校联合购买100套队服和a个足球，请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用；

    （3）假如你是本次购买任务的负责人，你认为到哪家商场购买比较合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=8，BC=6，点E在边AB上，点F在边CD上，点G、H在对角线AC上，若四边形EGFH是菱形，则AE的长是（ ）
    A.6
    B.6.25
    C.6.5
    D.7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把矩形纸片ABCD置于直角坐标系中，AB∥x轴，BC∥y轴，AB=4，BC=3，点B（5，1）翻折矩形纸片使点A落在对角线DB上的H处得折痕DG．

    （1）求AG的长；
    （2）在坐标平面内存在点M（m，﹣1）使AM+CM最小，求出这个最小值；
    （3）求线段GH所在直线的解析式．

    查看答案和解析>>

    同步练习册答案