
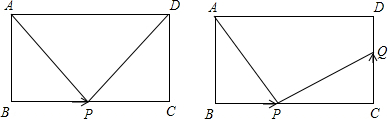
分析 (1)根据P点的运动速度可得BP的长;
(2)根据全等三角形的性质即可得出BP=CP即可;
(3)此题主要分两种情况①△ABP≌△PCQ得到BP=CQ,AB=PC,②△ABP≌△QCP得到BA=CQ,PB=PC,然后分别计算出t的值,进而得到v的值.
解答 解:(1)点P从点B出发,以2cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=2t,
则PC=14-2t;
(2)当t=$\frac{7}{2}$时,△ABP≌△DCP,
理由:∵BP=2t,CP=14-2t,
∵△ABP≌△DCP,
∴BP=CP,
∴2t=14-2t,
∴t=$\frac{7}{2}$,
(2)①当△ABP≌△PCQ时,
∴BP=CQ,AB=PC,
∵AB=8,
∴PC=8,
∴BP=BC-PC=14-8=6,
2t=6,
解得:t=3,
CQ=BP=6,
v×3=6,
解得:v=2;
②当△ABP≌△QCP时,
∴BA=CQ,PB=PC
∵PB=PC,
∴BP=PC=$\frac{1}{2}$BC=7,
2t=7,
解得:t=$\frac{7}{2}$,
CQ=BA=8,
v×$\frac{7}{2}$=8,
解得:v=$\frac{16}{7}$.
综上所述:当v=2或$\frac{16}{7}$时,△ABP与△PQC全等.
点评 此题是四边形综合题,主要考查了全等三角形的性质,矩形的性质,解本题的关键是全等三角形性质的掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24 cm2 | B. | 48 cm2 | C. | 24π cm2 | D. | 12π cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 加数的个数n | 连 续 偶 数 的 和 S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
| … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com