
单项式 的系数和次数分别是( )
的系数和次数分别是( )
A. 系数是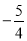 ,次数是3 B. 系数是
,次数是3 B. 系数是 ,次数是3
,次数是3
C. 系数是 ,次数是4 D. 系数是
,次数是4 D. 系数是 ,次数是4
,次数是4
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城市八年级(上)期末数学试卷(五四学制) 题型:填空题
当m=_____时,方程 =3的解为1.
=3的解为1.
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
定义一种新运算:a◎b=3a-2b+1,则当2◎x=5时,x的值是_______
_1_ 【解析】试题解析: 解得: 故答案为:1.查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年七年级上学期期终模拟数学试卷 题型:解答题
计算:(1) ;(2)
;(2) 
查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年七年级上学期期终模拟数学试卷 题型:单选题
运动会上,七年级(1)班的小王、小张、小李三人一起进行百米赛跑(假定三人均为匀速直线运动).如果当小李到达终点时,小张距终点还有4米,小王距终点还有12米.那么当小张到达终点时,小王距终点还有几米?
A. 8米 B.  米 C. 6米 D.
米 C. 6米 D. 
查看答案和解析>>
科目:初中数学 来源:人教版初中数学九年级上册第二十一章第一节《一元二次方程》同步测试(含答案) 题型:解答题
已知关于x的方程(m-n)x2+mx+n=0,你认为:
(1)当m和n满足什么关系时,该方程是一元二次方程?
(2)当m和n满足什么关系时,该方程是一元一次方程?
(1)当m≠n时,方程是一元二次方程;(2)当m=n且m≠0时,方程是一元一次方程 【解析】试题分析:(1)一元二次方程要求最高项次数为2且二次项系数不为0,由题,只要 即可确定方程为一元二次方程. (2)一元一次方程要求最高项次数为1且一次项系数不为0,所以当方程同时满足 时,即可确定方程为一元一次方程. 试题解析:(1)根据题意得:m-n≠0,解得:m≠n; (2)根据题意...查看答案和解析>>
科目:初中数学 来源:人教版初中数学九年级上册第二十一章第一节《一元二次方程》同步测试(含答案) 题型:填空题
若一元二次方程2x2+(k+8)x-(2k-3)=0的二次项系数、一次项系数、常数项之和为5,则k=________
8 【解析】试题分析:由题,二次项系数为2,一次项系数为 ,常数项为 , ,解得 . 所以本题的正确答案为8.查看答案和解析>>
科目:初中数学 来源:浙江杭州余杭区2016-2017学年八年级上学期期末数学试卷 题型:填空题
已知:  是
是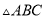 的
的 边上的中线,且
边上的中线,且 .若
.若 ,
,  ,则
,则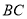 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.1.2 反比例函数的图象和性质 题型:解答题
如图,直线y=2x﹣6与反比例函数 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.
(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com