某书店正在销售一种课外读本,进价12元/本,售价20元/本,为了促销,书店决定凡是一次购买10本以上的客户,每多买一本,售价就降低0.10元,但最低价为16元/本.
(1)客户一次至少买多少本,才能以最低价购买?
(2)求当一次购买x本时(x>10),书店利润y(元)与购买量x(本)之间的函数关系式;
(3)在销售过程中,书店发现卖出50本比卖出46本赚的钱少,为了使每次的销售均能达到多卖出就多获利,在其他促销条件不变的情况下,最低价应确定为多少元/本?请说明理由.
【答案】
分析:(1)设客户一次购买x本,才能以最低价购买,然后根据降低的价钱列出方程求解即可;
(2)根据利润等于每本的盈利乘以购买的本数,分大于最低价与等于最低价两种情况列式整理即可得解;
(3)根据二次函数的最值问题确定出获利最多时卖出书本的本数即可得解.
解答:解:(1)设客户一次购买x本,才能以最低价购买,
即(x-10)×0.1=20-16,
解得x=50(本);
(2)当10<x≤50时,
y=[20-12-0.1(x-10)]•x=-0.1x
2+9x,
当x>50时,y=(16-12)•x=4x,
即y=
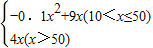
;
(3)当10<x≤50时,
y=-0.1x
2+9x=-0.1(x
2-90x)=-0.1(x-45)
2+202.5,
∵-0.1<0,
∴当x=45时,y
最大=202.5,
当45<x≤50时,y随x的增大而减小,
所以,卖出50本比卖出46本赚的钱少,
即必须把最低价定在销售数量为45本时的价格,才能使每次销售均赚钱,
20-0.1×(45-10)=20-3.5=16.5元,
即单价为16.5元.
点评:本题考查了二次函数的应用,主要利用了求分段函数的解析式,二次函数的增减性,理清题目数量关系,表示出利润y(元)与购买量x(本)之间的函数关系式是解题的关键.

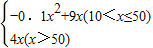 ;
;
