
如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)求证:四边形BMNP是平行四边形;
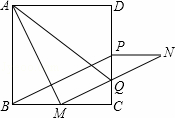
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
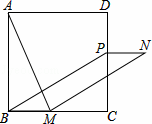
1)证明:在正方形ABCD中,AB=BC,∠ABC=∠B,
在△ABM和△BCP中,
 ,
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠BAM=∠CBP,
∵∠BAM+∠AMB=90°,
∴∠CBP+∠AMB=90°,
∴AM⊥BP,
∵AM并将线段AM绕M顺时针旋转90°得到线段MN,
∴AM⊥MN,且AM=MN,
∴MN∥BP,
∴四边形BMNP是平行四边形;
( 2)解:BM=MC.
2)解:BM=MC.
理由如下:∵∠BAM+∠AMB=90°,∠AMB+∠CMQ=90°,
∴∠BAM=∠CMQ,
又∵∠B=∠C=90°,
∴△ABM∽△MCQ,
∴ =
= ,
,
∵△MCQ∽△AMQ,
∴△AMQ∽△ABM,
∴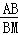 =
= ,
,
∴ =
=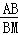 ,
,
∴BM=MC.


科目:初中数学 来源: 题型:
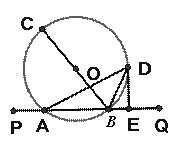
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E。
(1)求证:DE与⊙O相切;
(2)连结AD,己知BC=10,BE=2,求sinBAD的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
下面是扬帆中学九年级八班43名同学家庭人口的统计表:
| 家庭人口数(人) | 3 | 4 | 5 | 6 | 2 |
| 学生人数(人) | 15 | 10 | 8 | 7 | 3 |
这43个家庭人口的众数和中位数分别是
| A. | 5,6 | B. | 3,4 | C. | 3,5 | D. | 4,6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
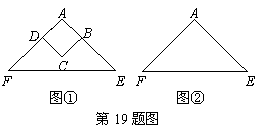
如图①,正方形ABCD的边AB,AD分别在等腰直角△AEF的腰AE,AF上,点C在△AEF内,则有DF=BE(不必证明).将正方形ABCD绕点A逆时针旋转一定角度α(0°<α<90°)后,连结BE,DF.请在图②中用实线补全图形,这时DF=BE还成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com