
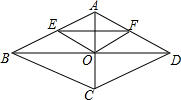
 如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.
如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.分析 (1)利用菱形的性质结合直角三角形斜边上的中线等于斜边的一半,进而求出即可;
(2)利用勾股定理得出BO的长再利用三角形中位线定理得出EF的长.
解答 解:(1)△OEF是等腰三角形,
理由:∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,
∵点E,F分别是边AB,AD的中点,
∴EO=$\frac{1}{2}$AB,OF=$\frac{1}{2}$AD,
∴EO=FO,
∴△OEF是等腰三角形;
(2)∵四边形ABCD是菱形,AC=10,
∴AO=5,∠AOB=90°,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴BD=24,
∵点E,F分别是边AB,AD的中点,
∴EF$\stackrel{∥}{=}$$\frac{1}{2}$BD,
∴EF=12.
点评 此题主要考查了菱形的性质以及勾股定理和三角形中位线定理等知识,熟练应用菱形的性质是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于点O成中心对称的△A″B″C″.
如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于点O成中心对称的△A″B″C″.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
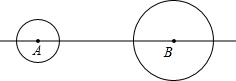 如图,在直线上有A、B两点,AB=10cm,⊙A的半径是1cm,⊙B的半径是2cm,⊙A以3cm/s的速度向右运动,同时⊙B以1cm/s的速度向右运动.设运动时间为t秒,当⊙A与⊙B相切时,t的值是3.5、4.5、5.5、6.5.
如图,在直线上有A、B两点,AB=10cm,⊙A的半径是1cm,⊙B的半径是2cm,⊙A以3cm/s的速度向右运动,同时⊙B以1cm/s的速度向右运动.设运动时间为t秒,当⊙A与⊙B相切时,t的值是3.5、4.5、5.5、6.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.7×10-5米 | B. | 77×10-6米 | C. | 77×10-5米 | D. | 7.7×10-6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
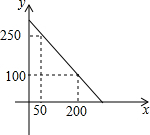 某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系式如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系式如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com