
 已知,如图,斜坡PQ坡度为i=1:
已知,如图,斜坡PQ坡度为i=1:| 4 | 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| AQ |
| tan∠ACQ |
| 4 | ||
|
| 16 |
| 3 |
| AC2+AQ2 |
(
|
| 20 |
| 3 |
| 20 |
| 3 |
| BC |
| tan∠BMC |
| 1 | ||
|
| 4 |
| 3 |
| 20 |
| 3 |
| 4 |
| 3 |

| 4 |
| 3 |


科目:初中数学 来源: 题型:
| 3 |
 为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.
为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,在坡面上点O处有一根1m高且垂直于水平面的水管OA,顶端A处有一旋转式喷头向外喷水,水流在各个方向沿相同的抛物线落下,水流最高点M比点A高出1m,且在点A测得点M的仰角为30°,以O点
,在坡面上点O处有一根1m高且垂直于水平面的水管OA,顶端A处有一旋转式喷头向外喷水,水流在各个方向沿相同的抛物线落下,水流最高点M比点A高出1m,且在点A测得点M的仰角为30°,以O点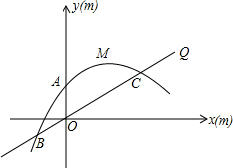 为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.
为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2009年第7届“学用杯”全国数学知识应用竞赛九年级初赛试卷(A卷)(解析版) 题型:填空题
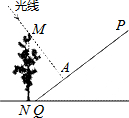
 ,坡脚Q旁的点N处有一棵大树MN.近中午的某个时刻,太阳光线正好与斜坡PQ垂直,光线将树顶M的影子照射在斜坡PQ上的点A处.如果AQ=4米,NQ=1米,则大树MN的高度为 .
,坡脚Q旁的点N处有一棵大树MN.近中午的某个时刻,太阳光线正好与斜坡PQ垂直,光线将树顶M的影子照射在斜坡PQ上的点A处.如果AQ=4米,NQ=1米,则大树MN的高度为 .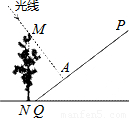
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com