
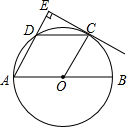
 如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.分析 (1)连接AC,由题意得$\widehat{AD}$=$\widehat{CD}$=$\widehat{CB}$,∠DAC=∠CAB,即可证明AE∥OC,从而得出∠OCE=90°,即可证得结论;
(2)四边形AOCD为菱形.由$\widehat{AD}$=$\widehat{CB}$,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形).
解答  解:(1)连接AC,
解:(1)连接AC,
∵点CD是半圆O的三等分点,
∴$\widehat{AD}$=$\widehat{CD}$=$\widehat{CB}$,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠CAB=∠OCA,
∴∠DAC=∠OCA,
∴AE∥OC(内错角相等,两直线平行)
∴∠OCE+∠E=180°,
∵CE⊥AD,
∴∠OCE=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)四边形AOCD为菱形.
理由是:
∵$\widehat{AD}$=$\widehat{CB}$,
∴∠DCA=∠CAB,
∴CD∥OA,
又∵AE∥OC,
∴四边形AOCD是平行四边形,
∵OA=OC,
∴平行四边形AOCD是菱形.
点评 本题考查了切线的判定、等腰三角形的性质、平行线的判定和性质、菱形的判定和性质,是中学阶段的重点内容.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章,记载了一道“折竹抵地”问题,叙述为:“今有竹高一丈,末折抵地,去本三尺,问折者几何?”翻译成数学问题是:在Rt△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,可列出的方程为x2+32=(10-x)2.
《九章算术》是我国古代最重要的数学著作之一,在“勾股”章,记载了一道“折竹抵地”问题,叙述为:“今有竹高一丈,末折抵地,去本三尺,问折者几何?”翻译成数学问题是:在Rt△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,可列出的方程为x2+32=(10-x)2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在选举中,人们通常最关心的数据是众数 | |
| B. | 数据3,5,4,1,-2的中位数是3 | |
| C. | 一组数据1,1,0,2,4的平均数为2 | |
| D. | 甲、乙两人数学成绩的平均分都是95,方差分别是2.5和10.5,要选择一人参加数学竞赛,选甲比较稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m<kx-1的解集在数轴上表示正确的是( )
如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m<kx-1的解集在数轴上表示正确的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com