
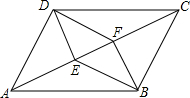
 如图,在平行四边形ABCD中,DE平分∠ADC交对角线AC于E,BF平分∠ABC交对角线AC于F,连接BE和DF.求证:四边形DEBF是平行四边形.
如图,在平行四边形ABCD中,DE平分∠ADC交对角线AC于E,BF平分∠ABC交对角线AC于F,连接BE和DF.求证:四边形DEBF是平行四边形. 分析 由平行四边形的性质得出∠ADC=∠ABC,AB=CD,AB∥CD,得出内错角相等∠BAF=∠DCE,再证出∠ABF=∠CDE,由ASA证明△ABF≌△CDE,得出BF=DE,∠AFB=∠CED,证出BF∥DE,即可得出四边形DEBF是平行四边形.
解答 证明:∵四边形ACD是平行四边形,
∴∠ADC=∠ABC,AB=CD,AB∥CD,
∴∠BAF=∠DCE,
∵DE平分∠ADC,BF平分∠ABC,
∴∠CDE=$\frac{1}{2}$∠ADC,∠ABF=$\frac{1}{2}$∠ABC,
∴∠ABF=∠CDE,
在△ABF和△CDE中,
$\left\{\begin{array}{l}{∠BAF=∠DCE}&{\;}\\{AB=CD}&{\;}\\{∠ABF=∠CDE}&{\;}\end{array}\right.$,
∴△ABF≌△CDE(ASA),
∴BF=DE,∠AFB=∠CED,
∴BF∥DE,
∴四边形DEBF是平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的判定与性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
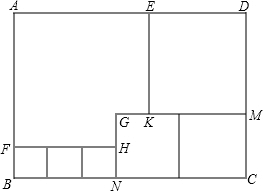 如图所示,用三种大小不等的正方形和一个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=GK=1,设BF=x.
如图所示,用三种大小不等的正方形和一个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=GK=1,设BF=x.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
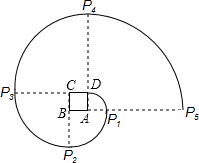 如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.
如图,正方形ABCD,曲线DP1P2P3P4P5…叫做“正方形的渐开线”,其中弧DP1,弧P1P2,弧P2P3,弧P3P4,弧P4P5…的圆心依次按点A,B,C,D,A循环,它们的弧长分别记为l1,l2,l3,l4,l5….当AB=1时,l2011等于$\frac{2011π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

| 长桌张数 | 1 | 2 | 3 | 4 | … | n |
| 可坐人数 | 6 | 8 | 10 | 12 | … | 2n+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 边数越多的多边形,它的内角和也越大 | |
| B. | 多边形随着边数的增加,它的外角和和随着增加 | |
| C. | 当多边形的边数扩大两倍时,多边形的内角和也扩大两倍 | |
| D. | 当边数超过4时,多边形的内角一定大于相邻的外角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )| A. | -2a | B. | 2a-2 | C. | 3-2a | D. | 2a-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com