

 解:(1)四边形EFGH的形状是平行四边形.
解:(1)四边形EFGH的形状是平行四边形. AC.在△ADC中,同样可以得到HG∥AC,HG=
AC.在△ADC中,同样可以得到HG∥AC,HG= AC.所以四边形EFGH是平行四边形.
AC.所以四边形EFGH是平行四边形.


科目:初中数学 来源: 题型:
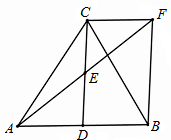 19、如图.在△ABC中,D是AB的中点.E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连接BF.
19、如图.在△ABC中,D是AB的中点.E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:
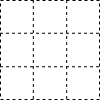 如图,用一块正方形纸板,在四个角上截去四个相同的边长为2cm的小正方形,然后把四边折起来,做成一个没有盖的长方体盒子,使它的容积为32cm3.所用的正方形纸板的边长应是多少厘米?如果设正方形纸板的边长是xcm,请列出方程,并把它化成一般形式.
如图,用一块正方形纸板,在四个角上截去四个相同的边长为2cm的小正方形,然后把四边折起来,做成一个没有盖的长方体盒子,使它的容积为32cm3.所用的正方形纸板的边长应是多少厘米?如果设正方形纸板的边长是xcm,请列出方程,并把它化成一般形式.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:黄冈难点课课练 八年级数学上册 题型:013
如图,正方形(四边都相等,四个角都是直角)的边长为1,如果将线段BD绕着点B旋转后,点D落在BC延长线上的点![]() 处,则
处,则![]() 的长为
的长为

[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com