
【题目】如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
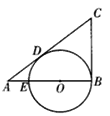
【答案】(1)BE=6;(2) S△ABC=24..
【解析】
(1)连接OD,由切线的性质得OD⊥AC,,在Rt△ODA中运用勾股定理可以求出半径OD,即可求得直径BE的长;
(2)由切线长定理知,CD=BC,在Rt△ABC中运用勾股定理可以求出BC,则可由直角三角形的面积公式求得△ABC的面积.
(1)连接OD,

∴OD⊥AC
∴△ODA是直角三角形
设半径为r
∴AO=r+2
∴![]()
解之得:r=3
∴BE=6
(2)∵∠ABC=900
∴OB⊥BC
∴BC是⊙O的切线
∵CD切⊙O于D
∴CB=CD
令CB=x
∴AC=x+4, CB=x,AB=8
∵![]()
∴x=6.
∴S△ABC=![]() 24(cm2).
24(cm2).
故答案为:(1)BE=6;(2) S△ABC=24..


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
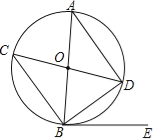
【题目】如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+3与x轴相交于点A,与y轴相交于点B,点C是第二象限内任意一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
x+3与x轴相交于点A,与y轴相交于点B,点C是第二象限内任意一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)如图①,当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径r;
(3)在⊙C的移动过程中,能否使△OEF是等边三角形?(只回答“能”或“不能”)

查看答案和解析>>
科目:初中数学 来源: 题型:
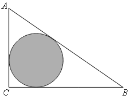
【题目】如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
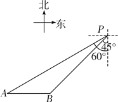
【题目】如图,一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com