
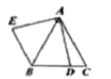
【题目】如图,![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 是直线
是直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 在点
在点![]() 运动过程中,线段
运动过程中,线段![]() 的最小值为____.
的最小值为____.
【答案】![]()
【解析】
首先根据题意找到点E的运动轨迹是一条直线,然后根据垂线段最短确定BE的最小值,最后利用勾股定理及矩形性质计算即可
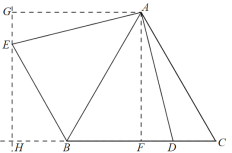
解:如图,过点A作AF⊥BC于点F,将AF绕点A顺时针旋转90°得到线段AG,连接GE并延长交CB的延长线于点H
∵AF⊥BC,
∴∠AFD=∠AFB=90°,
∵![]() 是边长为2的等边三角形,AF⊥BC,
是边长为2的等边三角形,AF⊥BC,
∴BF=![]() BC=1
BC=1
在Rt△ABC中,![]()
∵旋转
∴∠GAF=∠EAD=90°,AG=AF,AE=AD,
∴∠GAE=∠FAD,
∴△GAE≌△FAD(SAS)
∴∠AGE=∠AFD=90°,
∵点D在直线BC上运动
∴点E在直线GE上运动
∴当BE⊥GE时,BE最短
∵∠GAF=∠AFD=∠AGE =90°,AG=AF
∴四边形AGHF为正方形
∴HF=AF=![]() ,∠GHB=90°
,∠GHB=90°
∴当点E与点H重合时,BE取得最小值
∵HF=![]() ,BF=1
,BF=1
∴BH=HF-BF=![]()
即BE的最小值为![]()


科目:初中数学 来源: 题型:
【题目】下列命题中,(1)数轴上的所有点都表示有理数;(2)无理数可以用数轴上的点表示;(3)实数与数轴上的点一一对应;(4)无限小数是无理数;(5)带根号的数都是无理数;(6)数轴上的点不是表示有理数,就是表示无理数;错误命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末,历史老师为了了解所任教的甲、乙两班学生的历史基础知识背诵情况,从甲、乙两个班学生中分别随机抽取了20名学生来进行历史基础知识背诵检测,满分50分,得到学生的分数相关数据如下:
甲 | 32 | 35 | 46 | 23 | 41 | 49 | 37 | 41 | 36 | 41 |
37 | 44 | 39 | 46 | 46 | 41 | 50 | 43 | 44 | 49 |
乙 | 25 | 34 | 43 | 46 | 35 | 41 | 42 | 46 | 44 | 42 |
47 | 45 | 42 | 34 | 39 | 47 | 49 | 48 | 45 | 42 |
通过整理,分析数据:两组数据的平均数、中位数、众数如下表:
平均数(分) | 中位数(分) | 众数(分) | |
甲 | 41 | 41 |
|
乙 | 41.8 |
| 42 |
历史老师将乙班成绩按分数段(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示分数)绘制成扇形统计图,如图(不完整)
表示分数)绘制成扇形统计图,如图(不完整)
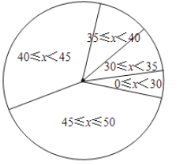
请回答下列问题:
(1)![]() _______分;
_______分;
(2)扇形统计图中,![]() 所对应的圆心角为________度;
所对应的圆心角为________度;
(3)请结合以上数据说明哪个班背诵情况更好(列举两条理由即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践 问题情境:
综合与实践课上,同学们以“三角形纸片的折叠与旋转“为主题展开数学活动,探究有关的数学问题.
动手操作:
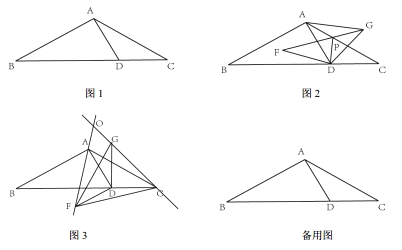
已知:三角形纸片![]() 中,
中,![]() .将三角形纸片
.将三角形纸片![]() 按如下步骤进行操作:
按如下步骤进行操作:
第一步:如图1,折叠三角形纸片![]() ,使点
,使点![]() 与点
与点![]() 重合,然后展开铺平,折痕分别交
重合,然后展开铺平,折痕分别交![]() 于点
于点![]() ,连接
,连接![]() ,易知
,易知![]() .
.
第二步:在图1的基础上,将三角形纸片![]() 沿
沿![]() 剪开,得到
剪开,得到![]() 和
和![]() .保持
.保持![]() 的位置不变,将
的位置不变,将![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() (点
(点![]() 分别是
分别是![]() 的对应点),旋转角为
的对应点),旋转角为![]() 问题解决:
问题解决:
(1)如图2,小彬画出了旋转角![]() 时的图形,设线段
时的图形,设线段![]() 交于点
交于点![]() ,连接
,连接![]() .小彬发现
.小彬发现![]() 所在直线始终垂直平分线段
所在直线始终垂直平分线段![]() .请证明这一结论;
.请证明这一结论;
(2)如图3,小颖画出了旋转角![]() 时的图形,设直线
时的图形,设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() 判断此时
判断此时![]() 的形状,说明理由;
的形状,说明理由;
(3)在![]() 绕点
绕点![]() 逆时针旋转过程中,当
逆时针旋转过程中,当![]() 时,请直接写出
时,请直接写出![]() 两点间的距离.
两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com