
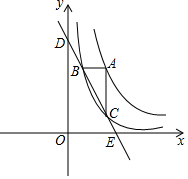
 如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数y=$\frac{4}{x}$(x>0)图象上运动时,
如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数y=$\frac{4}{x}$(x>0)图象上运动时,分析 (1)由条件可先求得A点坐标,从而可求得B点纵坐标,再代入y=$\frac{1}{x}$可求得B点与C点的坐标;
(2)可设出A点坐标,从而可表示出C、B的坐标,则可表示出AB和AC的长,可求得△ABC的面积;
(3)可证明△ABC∽△EFC,利用(2)中,AB和AC的长可表示出EF,可得到BG=EF,从而可证明△DBG≌△CFE,可得到DB=CF.
解答 解:(1)∵点A横坐标为a,点A在函数y=$\frac{4}{x}$(x>0)图象上,
∴点A纵坐标为$\frac{4}{a}$,
∵AB∥x轴,AC∥y轴,
∴点B的纵坐标为:$\frac{4}{a}$,点C的横坐标a,
∴点B横坐标为:$\frac{1}{4}$a;点C的纵坐标为:$\frac{1}{a}$,
∴B点坐标为($\frac{1}{4}$a,$\frac{4}{a}$),C(a,$\frac{1}{a}$);
故答案为:($\frac{1}{4}$a,$\frac{4}{a}$),C(a,$\frac{1}{a}$);
(2)∵A(a,$\frac{4}{a}$),则C(a,$\frac{1}{a}$),B($\frac{a}{4}$,$\frac{4}{a}$),
∴AB=a-$\frac{a}{4}$=$\frac{3}{4}$a,AC=$\frac{4}{a}$-$\frac{1}{a}$=$\frac{3}{a}$,
∴S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×$\frac{3}{4}$a×$\frac{3}{a}$=$\frac{9}{8}$,
即△ABC的面积不发生变化,其面积为$\frac{9}{8}$;
(3)BD=CE,
如图,设AB的延长线交y轴于点G,AC的延长线交x轴于点F,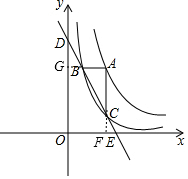
∵AB∥x轴,
∴△ABC∽△EFC,
∴$\frac{AB}{EF}$=$\frac{AC}{FC}$,即$\frac{\frac{3}{4}a}{EF}$=$\frac{\frac{3}{a}}{\frac{1}{a}}$,
∴EF=$\frac{1}{4}$a,
由(2)可知BG=$\frac{1}{4}$a,
∴BG=EF,
∵AE∥y轴,
∴∠BDG=∠FCE,
在△DBG和△CFE中$\left\{\begin{array}{l}{∠BDG=∠FCE}\\{∠BGD=∠FEC}\\{BG=EF}\end{array}\right.$,
∴△DBG≌△CEF(AAS),
∴BD=CE.
点评 本题为反比例函数的综合应用,涉及函数图象的交点、平行线的性质、三角形的面积、相似三角形的判定和性质、全等三角形的判定和性质等知识.要(1)中求得A点坐标是解题的关键,在(2)中用a表示出AB、AC的长是解题的关键,在(3)中证得BD=EC,构造三角形全等是解题的关键.本题考查知识点较多,综合性较强,难度适中.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | x>23 | B. | 23<x≤47 | C. | 11≤x<23 | D. | x≤47 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com