
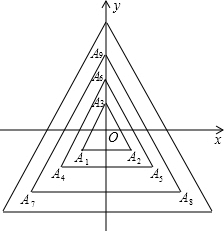
 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是(-673,-673).
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是(-673,-673). 分析 先根据每一个三角形有三个顶点确定出A2017所在的三角形,再求出相应的三角形的边长以及A2017的纵坐标的长度,即可得解.
解答 解:∵2017÷3=672…1,
∴A2017是第673个等边三角形的第1个顶点,
第673个等边三角形边长为2×673=1346,
∴点A2017的横坐标为 $\frac{1}{2}$×(-1346)=-673,
∵边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,
∴点A2017的纵坐标为-673,
∴点A2014的坐标为(-673,-673),
故答案为:(-673,-673).
点评 本题考查了点的坐标、等边三角形的性质,是点的变化规律,主要利用了等边三角形的性质,确定出点A2017所在三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
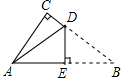 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )| A. | 4 cm | B. | 5 cm | C. | 6 cm | D. | 10 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,那么S3=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)3,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,那么S3=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)3,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 初三某班学生去中央公园踏青,班级信息员骑自行车先从学校出发,5分钟后其余同学以60米/分的速度从学校向公园行进,信息员先到达公园后用5分钟找到聚集地点,再立即按原路以另一速度返回到队伍汇报聚集地点,最后与同学们一起步行到公园,信息员离其余同学的距离y(米)与信息员出发的时间x(分)之间的关系如图所示,则信息员开始返回之后,再经过3分钟与其余同学相距720米.
初三某班学生去中央公园踏青,班级信息员骑自行车先从学校出发,5分钟后其余同学以60米/分的速度从学校向公园行进,信息员先到达公园后用5分钟找到聚集地点,再立即按原路以另一速度返回到队伍汇报聚集地点,最后与同学们一起步行到公园,信息员离其余同学的距离y(米)与信息员出发的时间x(分)之间的关系如图所示,则信息员开始返回之后,再经过3分钟与其余同学相距720米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
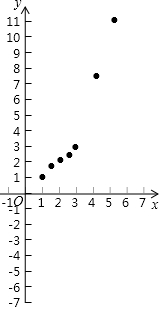 有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.
有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.| x | … | -$\frac{1}{2}$ | 0 | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | $\frac{9}{2}$ | … |
| y | … | -$\frac{113}{16}$ | -3 | 1 | $\frac{27}{16}$ | 2 | $\frac{37}{16}$ | 3 | 7 | $\frac{177}{16}$ | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com