
【题目】如图,已知抛物线y1=x2-2x-3与x轴相交于点A,B(点A在B的左侧),与y轴相交于点C,直线y2=kx+b经过点B,C.

(1)求直线BC的函数关系式;
(2)当y1>y2时,请直接写出x的取值范围.
科目:初中数学 来源: 题型:
【题目】如图![]() 某种三角形台历被放置在水平桌面上,其左视图如图
某种三角形台历被放置在水平桌面上,其左视图如图![]() ,其中点
,其中点![]() 是台历支架
是台历支架![]() 、
、![]() 的交点,同时又是台历顶端连接日历的螺旋线圈所在圆的圆心.现测得
的交点,同时又是台历顶端连接日历的螺旋线圈所在圆的圆心.现测得![]() ,
,![]() ,
,![]() .
.
![]() 求点
求点![]() 到直线
到直线![]() 的距离;
的距离;
![]() 求张角
求张角![]() 的大小;
的大小;
![]() 现把某月的日历从台历支架正面翻到背面(即
现把某月的日历从台历支架正面翻到背面(即![]() 与
与![]() 重合),求点
重合),求点![]() 所经历的路径长.
所经历的路径长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 取
取![]() ,所有结果精确到
,所有结果精确到![]() ,可使用科学计算器)
,可使用科学计算器)

查看答案和解析>>
科目:初中数学 来源: 题型:
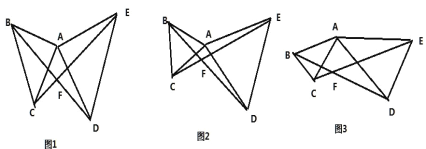
【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去离家2.4 km的体育馆看球赛,进场时,发现门票还放在家中,此时离比赛还有45 min,于是他立即步行(匀速)回家取票,在家取票用时2 min,取到票后,他马上骑自行车(匀速)赶往体育馆.已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少20 min,骑自行车的速度是步行速度的3倍.
(1)小明步行的速度是多少?
(2)小明能否在球赛开始前赶到体育馆?
查看答案和解析>>
科目:初中数学 来源: 题型:
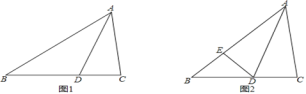
【题目】在△ABC中,AD是它的角平分线.
(1)如图1,求证:S△ABD:S△ACD=AB:AC=BD:CD;
(2)如图2,E是AB上的点,连接ED,若BD=3,BE=CD=2,AE=2CD,求证:△BED是等腰三角形;
(3)在图1中,若3∠BAC=2∠C,∠ADB>∠B>∠BAD,直接写出∠BAC的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com