
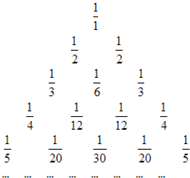
 如图所示的数阵叫“莱布尼兹调和三角形”,它们是由正整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如:$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$…,那么第7行第3个数字是$\frac{1}{105}$.
如图所示的数阵叫“莱布尼兹调和三角形”,它们是由正整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如:$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$…,那么第7行第3个数字是$\frac{1}{105}$. 分析 根据每个数是它下一行相邻两数的和,求出第5、6、7三行的第二个数,继而可得第7行的第3个数.
解答 解:设第n行第m个数为a(n,m),
由题意知a(6,1)=$\frac{1}{6}$,a(7,1)=$\frac{1}{7}$,
∴a(7,2)=a(6,1)-a(7,1)=$\frac{1}{6}$-$\frac{1}{7}$=$\frac{1}{42}$,
a(6,2)=a(5,1)-a(6,1)=$\frac{1}{5}$-$\frac{1}{6}$=$\frac{1}{30}$,
a(7,3)=a(6,2)-a(7,2)=$\frac{1}{30}$-$\frac{1}{42}$=$\frac{1}{105}$,
故答案为:$\frac{1}{105}$.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
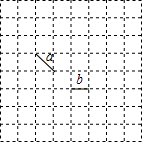 如图是8×8的格点,线段a、b的端点在格点上,请在图中画出第三条线段,使其端点在格点上且与线段a、b组成轴对称图形.(画出所有情况,并在图中把这些线段标记为线段c、d、e、f、g….)
如图是8×8的格点,线段a、b的端点在格点上,请在图中画出第三条线段,使其端点在格点上且与线段a、b组成轴对称图形.(画出所有情况,并在图中把这些线段标记为线段c、d、e、f、g….)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
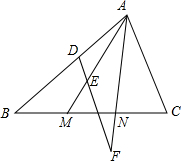 如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求$\frac{EF}{DE}$的值.
如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求$\frac{EF}{DE}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0,?△>0 | B. | a>0,?△<0 | C. | a<0,?△>0 | D. | a<0,?△<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com