
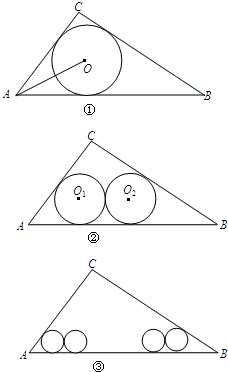
 在△ABC中,已知∠C=90°,AC=6,BC=8.
在△ABC中,已知∠C=90°,AC=6,BC=8.分析 (1)连接三角形的内心和三角形的各个顶点,根据三角形的总面积等于分割成的三个小三角形的面积,进行计算;
(2)连接两圆的圆心和每个圆的圆心和三角形的三个顶点,把大三角形分割成了三个三角形和一个梯形,根据三角形的总面积等于四部分的面积的和,进行计算;
(3)连接第一个圆和最后一个圆的圆心,以及两个圆的圆心和三角形的三个顶点,根据(2)的思路进行计算.
解答 解:(1)∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10.
如图1,设⊙O1与Rt△ABC的边AB,BC,CA分别切于点D,E,F.
连接O1D,O1E,O1F,AO1,BO1,CO1.
于是O1D⊥AB,O1E⊥BC,O1F⊥AC.
S${\;}_{△A{O}_{1}C}$=$\frac{1}{2}$AC•O1F=$\frac{1}{2}$AC•r1=3r1,S${\;}_{△B{O}_{1}C}$=$\frac{1}{2}$BC•O1E=$\frac{1}{2}$BC•r1=4r1,S${\;}_{△A{O}_{1}B}$=$\frac{1}{2}$AB•O1D=$\frac{1}{2}$AB•r1=5r1,S△ABC=$\frac{1}{2}$AC•BC=24.
又∵S△ABC=S${\;}_{△A{O}_{1}C}$△AO1C+S${\;}_{△B{O}_{1}C}$+S${\;}_{△A{O}_{1}B}$,
∴24=3r1+4r1+5r1,
∴r1=2.
(2)如图2,连接AO1,BO2,CO1,CO2,O1O2,则
S${\;}_{△A{O}_{1}C}$=$\frac{1}{2}$AC•r2=3r2,S${\;}_{△B{O}_{2}C}$=$\frac{1}{2}$BC•r2=4r2.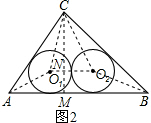
∵等圆⊙O1,⊙O2外切,
∴O1O2=2r2,且O1O2∥AB.
过点C作CM⊥AB于点M,交O1O2于点N,则
CM=$\frac{AC•BC}{AB}$=$\frac{24}{5}$,CN=CM-r2=$\frac{24}{5}$-r2.
∴S${\;}_{△C{O}_{1}{O}_{2}}$=$\frac{1}{2}$O1O2•CN=( $\frac{24}{5}$-r2)r2,
∴S${\;}_{梯形A{O}_{1}{O}_{2}B}$=$\frac{1}{2}$(2r2+10)r2=(r2+5)r2.
∵S△ABC=S${\;}_{△A{O}_{1}C}$+S${\;}_{△B{O}_{2}C}$+S${\;}_{△C{O}_{1}{O}_{2}}$+S${\;}_{梯形A{O}_{1}{O}_{2}B}$,
∴3r2+4r2+( $\frac{24}{5}$-r2)•r2+(r2+5)r2=24,
解得r2=$\frac{10}{7}$.
(3)如图3,连接AO1,BOn,CO1,COn,O1On,则
S${\;}_{△A{O}_{1}C}$=$\frac{1}{2}$AC•rn=3rn,S${\;}_{△B{O}_{n}C}$=$\frac{1}{2}$BC•rn=4rn.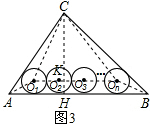
∵等圆⊙O1,⊙O2,…,⊙On依次外切,且均与AB边相切,
∴O1,O2,…,On均在直线O1On上,且O1On∥AB,
∴O1On=(n-2)2rn+2rn=2(n-1)rn.
过点C作CH⊥AB于点H,交O1On于点K,
则CH=$\frac{24}{5}$,CK=$\frac{24}{5}$-rn.
S${\;}_{△C{O}_{1}{O}_{n}}$=$\frac{1}{2}$O1On•CK=(n-1)( $\frac{24}{5}$-rn)rn,S${\;}_{梯形A{O}_{1}{O}_{n}B}$=$\frac{1}{2}$[2(n-1)rn+10]rn=[(n-1)rn+5]rn.
∵S△ABC=S${\;}_{△A{O}_{1}C}$+S${\;}_{△C{O}_{1}{O}_{n}}$+S${\;}_{△C{O}_{1}{O}_{n}}$+S${\;}_{梯形A{O}_{1}{O}_{n}B}$,
∴24=3rn+4rn+(n-1)( $\frac{24}{5}$-rn)rn+[(n-1)rn+5]rn.
解得rn=$\frac{10}{2n+3}$.
点评 本题考查圆的有关知识,三角形内切圆,两圆位置关系等知识,解决此题的方法是根据三角形的面积的不同计算方法进行计算,学会利用面积法求直角三角形斜边上的高,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 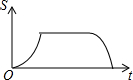 | B. | 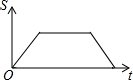 | C. |  | D. | 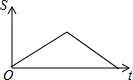 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 红星中学为了解七年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
红星中学为了解七年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:| 发言次数n | |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知正方形A1B1C1D1的面积为1,把它的各边延长一倍得到新的正方形A2B2C2D2,再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3,以此下去…,则正方形A9B9C9D9的周长是2500.
如图,已知正方形A1B1C1D1的面积为1,把它的各边延长一倍得到新的正方形A2B2C2D2,再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3,以此下去…,则正方形A9B9C9D9的周长是2500.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com