
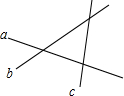
 如图,直线a,b,c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的站址有几处?如何选?请作简要说明并画出图形.
如图,直线a,b,c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的站址有几处?如何选?请作简要说明并画出图形. 分析 由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
解答 解:∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点P1满足条件;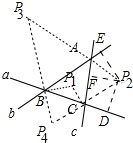 如图:点P2是△ABC两条外角平分线的交点,
如图:点P2是△ABC两条外角平分线的交点,
过点P2作P2E⊥AB,P2D⊥BC,P2F⊥AC,
∴P2E=P2F,P2F=P2D,
∴P2E=P2F=P2D,
∴点P2到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点P2到其三边的距离也相等,满足这条件的点有3个,如图P2、P3、P4.
综上所述:到三条公路的距离相等的点有4个,
故可供选择的地址有4个.
点评 此题考查了角平分线的性质.注意掌握角平分线上的点到角两边的距离相等,注意数形结合思想的应用,小心别漏解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
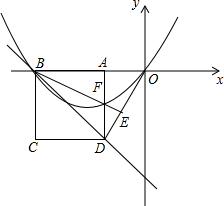 在平面直角坐标系中,已知点B(-2$\sqrt{2}$,0),A(m,0)($-\sqrt{2}<m<0$)以AB为边在x轴下方作正方形ABCD,连结OD,过B作BE垂直于OD于E,与AD相交于点F.
在平面直角坐标系中,已知点B(-2$\sqrt{2}$,0),A(m,0)($-\sqrt{2}<m<0$)以AB为边在x轴下方作正方形ABCD,连结OD,过B作BE垂直于OD于E,与AD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
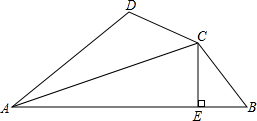 如图,四边形ABCD中,AC平分∠BAD,∠ADC+∠ABC=180°,CE⊥AB于E,猜想AD、AE、AB之间的关系式,并证明你的猜想.
如图,四边形ABCD中,AC平分∠BAD,∠ADC+∠ABC=180°,CE⊥AB于E,猜想AD、AE、AB之间的关系式,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,对角线的长为2,动点P沿对角线BD从点B开始向点D运动,到达点D后停止运动.设BP=x,△PBC的面积为S,试确定S与x之间的函数表达式,并写出x的取值范围.
如图,在正方形ABCD中,对角线的长为2,动点P沿对角线BD从点B开始向点D运动,到达点D后停止运动.设BP=x,△PBC的面积为S,试确定S与x之间的函数表达式,并写出x的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com