
【题目】如图,已知AB∥CD,请分别判断下面四个图形中∠APC、∠PAB、∠PCD之间的关系.
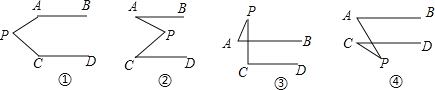
(1)写出相应的四个结论;
(2)请证明你所得的第③个图形的结论.
【答案】(1)①∠APC+∠PAB+∠PCD=360°,
②∠APC=∠PAB+∠PCD,
③∠APC=∠PCD﹣∠PAB,
④∠APC=∠PAB﹣∠PCD;
(2)见解析
【解析】
试题分析:分别过点P作PE∥AB,然后根据平行线的性质解答即可.
(1)解:①∠APC+∠PAB+∠PCD=360°,
②∠APC=∠PAB+∠PCD,
③∠APC=∠PCD﹣∠PAB,
④∠APC=∠PAB﹣∠PCD;
(2)证明:如图,过点P作PE∥AB,
∴∠APE=180°﹣∠PAB,
∵AB∥CD,
∴PE∥CD,
∴∠CPE=180°﹣∠PCD,
∴∠APC=∠APE﹣∠CPE=(180°﹣∠PAB)﹣(180°﹣∠PCD)=∠PCD﹣∠PAB.



科目:初中数学 来源: 题型:
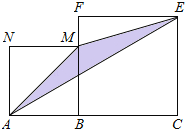
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
S3;则S3﹣S2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上的位置如图所示,其中点A对应的有理数为-4,且AB=10。动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒(t>0)。

(1)当t=1时,AP的长为_________,点P表示的有理数为______;
(2)当PB=2时,求t的值;
(3)M为线段AP的中点,N为线段PB的中点. 在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 相等的两个角是对顶角
B. 同位角相等
C. 图形平移后的大小可以发生改变
D. 两条直线相交所成的四个角都相等,则这两条直线互相垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com