Question

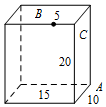
11．长方体的长为15，宽为10，高为20，点B在棱上与点C的距离为5，如图，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，则需要爬行的最短距离是（　　）

• A． $10\sqrt{5}+5$
• B． $5\sqrt{29}$
• C． 25
• D． $5\sqrt{37}$

Answer 1

分析 要求长方体中两点之间的最短路径，最直接的作法，就是将长方体侧面展开，然后利用两点之间线段最短解答．

解答 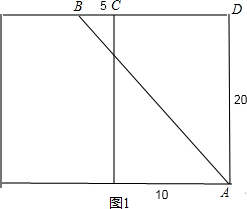解：只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形，如第1个图：
∵长方体的宽为10，高为20，点B离点C的距离是5，
∴BD=CD+BC=10+5=15，AD=20，
在直角三角形ABD中，根据勾股定理得：
∴AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\sqrt{1{5}^{2}+2{0}^{2}}$=25；
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如第2个图：
∵长方体的宽为10，高为20，点B离点C的距离是5，
∴BD=CD+BC=20+5=25，AD=10，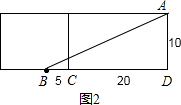

在直角三角形ABD中，根据勾股定理得：
∴AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\sqrt{1{0}^{2}+2{5}^{2}}$=5$\sqrt{29}$；
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形，如第3个图：
∵长方体的宽为10，高为20，点B离点C的距离是5，
∴AC=CD+AD=20+10=30，
在直角三角形ABC中，根据勾股定理得：
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{3{0}^{2}+{5}^{2}}$=5$\sqrt{37}$；
∵25＜5$\sqrt{29}$＜5$\sqrt{37}$，
∴蚂蚁爬行的最短距离是25．
故选C．

点评 本题主要考查两点之间线段最短，关键是将长方体侧面展开，然后利用两点之间线段最短解答．