
【题目】学校组织中国共产党第十九次全国代表大会知识问答,共设有20道选择题,各题分值相同,每题必答.下表记录了A、B、D三名参赛学生的得分情况:
参赛学生 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
D | 14 | 6 | 64 |
则参赛学生E的得 分可能 是( )
A.93B.87C.66D.40
【答案】D
【解析】
根据表格中3名参赛学生的得分情况,可知答对一题得5分,答错一题扣1分,设参赛学生E答对x道题(0≤x≤20,且x为整数),则其得分值为:5x-(20-x),然后逐个选项进行计算,结果符合x的取值范围的为正确答案.
解:根据表格数据,A学生答对20道得分100,由B、D同学得分情况可知答错一题扣1分,
故设参赛学生E答对x道题(0≤x≤20,且x为整数),则其得分值为:5x-(20-x)
选项A:令5x-(20-x)=93,解得x=![]() ,故A错误;
,故A错误;
选项B:令5x-(20-x)=87,解得x=![]() ,故B错误;
,故B错误;
选项C:令5x-(20-x)=66,解得x=![]() ,故C错误;
,故C错误;
选项D:令5x-(20-x)=40,解得x=10,故D正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】甲、乙两人从A地出发前往B地,甲先出发1分钟后,乙再出发,乙出发一段时间后返回A地取物品,甲、乙两人同时达到B地和A地,并立即掉头相向而行直至相遇,甲、乙两人之间相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则甲、乙两人最后相遇时,乙距B地的路程是_____米.
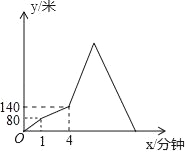
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
材料1:对称,也许是中国人最喜欢的。建筑师梁思成曾说过:“无论东方、西方,再没有一个民族对中轴对称线如此钟爱与恪守。”放眼中国的建筑,无论是宫殿、庙宇、亭台、楼阁、园林无不有着对称之美。数学世界也里有一些正整数你无论从左往右看,还是从右往左看,数字都是完全一样的,例如:11、101、2332、1234321、…,像这样的数我们叫它“对称数”.
材料2:如果一个三位数![]() ,满足a+b+c=8,我们就称这个三位数为“发财数”.
,满足a+b+c=8,我们就称这个三位数为“发财数”.
(1)请直接写出既是“对称数”又是“发财数”的所有三位数;
(2)一个三位“对称数”十位数字为7,它的各数位上的数字之和是一个自然数的平方,求这个三位数(请写出必要的推理过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|=6+7;|6-7|=7-6;|7-6|=7-6;|-6-7|=6+7;
根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=_________;
(2)|-![]() +0.8|=____________;
+0.8|=____________;
(3)|![]() |=__________;
|=__________;
(4)用合理的方法计算:|![]() |+|
|+|![]() |-|-
|-|-![]() |-
|-![]() ×|-
×|-![]() |+
|+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①![]() ,②
,②![]() ,③
,③![]() 三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.

(1)这三个命题中,真命题的个数为________;
(2)选择一个真命题,并且证明.(要求写出每一步的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班进行了一次数学測验,将成绩绘制成频数分布表和频数直方图的一部分如下:
成绩 | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
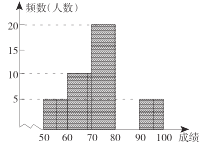
(1)在频数分布表中,![]() 的值为________,
的值为________,![]() 的值为________;
的值为________;
(2)将频数直方图补充完整;
(3)成绩在![]() 分以上(含
分以上(含![]() )的学生人数占全班总人数的百分比是多少?
)的学生人数占全班总人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
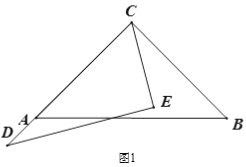
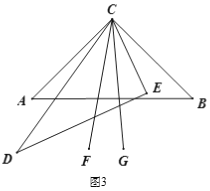
【题目】已知将一副三角板(直角三角板ABC和直角三角板CDE,∠ACB=90°,∠ECD=60°)如图1摆放,点D、A、C在一条直线上,将直角三角板CDE绕点C逆时针方向转动,变化摆放如图位置.
(1) 如图2,当∠ACD为多少度时,CB恰好平分∠ECD?
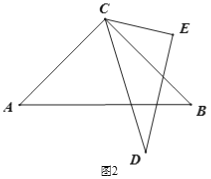
(2) 如图3,当三角板CDE摆放在∠ACB内部时,作射线CF平分∠ACE,射线CG平分∠BCD,如果三角形CDE在∠ACB内绕点C任意转动,∠FCG的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
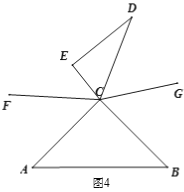
(3) 如图4,当三角板CDE转到∠ACB外部时,射线CF、CG仍然分别平分∠ACE、∠BCD,在旋转过程中,(2)中的结论是否成立?如果结论成立,请说明理由;如果不成立,请写出你的结论并根据图4说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com