Question

1．在矩形ABCD中AB=4，BC=6，点M为AD上一动点，连BM．
（1）如图1，作MN⊥BM交CD于N时，连BN，当DN最长时，证明：∠ABM=∠MBN；
（2）如图2，过点C作CP⊥BM于P点，将CP绕点C逆时针转90°到CQ，若点Q在AD延长线上时，求证：BM²=AB•BC；
（3）如图3，直接写出△MBC内切圆的半径的最大值．

Answer 1

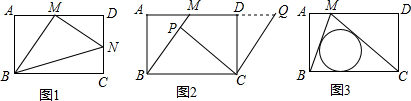
分析 （1）延长BA、NM交于点E，如图1．设AM=x，则DM=6-x．易证△ABM∽△DMN，根据相似三角形的性质可得到DN是x的二次函数，根据二次函数的最值性可得：当x=3时DN取最大值，此时AM=DM．易证△AEM≌△DNM，则有EM=NM．根据垂直平分线的性质可得BE=BN，根据等腰三角形的性质可得∠ABM=∠MBN；
（2）如图2，易证四边形BCQM是平行四边形，从而可得BM=CQ=CP．易证△BAM∽△CPB，根据相似三角形的性质可得$\frac{BM}{CB}$=$\frac{BA}{CP}$，再根据CP=BM，即可得到BM²=AB•BC；
（3）根据设△MBC内切圆的半径为r，根据等积法可得S_△MBC=$\frac{1}{2}$BC•AB=$\frac{1}{2}$（MB+MC+BC）•r，可得r=$\frac{24}{MB+MC+BC}$．由于BC已知，要求r的最大值，只需求MB+MC的最小值，延长BA到点B′，使得AB′=AB，连接MB′，如图3，易得MB+MC=MB′+MC．根据两点之间线段最短可得；当B′、M、C三点共线时，MB+MC取到最小值，即B′C长，只需在Rt△B′BC中运用勾股定理求出B′C，就可解决问题．

解答 解：（1）延长BA、NM交于点E，如图1．

设AM=x，则DM=6-x．
∵四边形ABCD是矩形，
∴∠BAD=∠D=90°，
∴∠ABM+∠AMB=90°．
∵MN⊥BM，∠BMN=90°，
∴∠AMB+∠DMN=180°-90°=90°，
∴∠ABM=∠DMN，
∴△ABM∽△DMN，
∴$\frac{AB}{DM}$=$\frac{AM}{DN}$，
∴$\frac{4}{6-x}$=$\frac{x}{DN}$，
∴DN=$\frac{1}{4}$x（6-x）=-$\frac{1}{4}$（x²-6x）
=-$\frac{1}{4}$[（x-3）²-9]=-$\frac{1}{4}$（x-3）²+$\frac{9}{4}$．
∵-$\frac{1}{4}$＜0，
∴当x=3时，DN取最大值，此时AM=DM=3．
∵四边形ABCD是矩形，
∴AB∥DC，
∴∠E=∠MND．
在△AEM和△DNM中，
$\left\{\begin{array}{l}{∠E=∠MND}\\{∠AME=∠DMN}\\{AM=DM}\end{array}\right.$，
∴△AEM≌△DNM，
∴EM=NM．
∵MN⊥BM，
∴BE=BN，
∴∠ABM=∠MBN；

（2）如图2，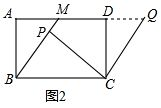

∵CP⊥BM，∠PCQ=90°，
∵∠BPC=∠PCQ=90°，
∴BM∥CQ．
∵四边形ABCD是矩形，
∴AD∥BC，即MQ∥BC，
∴四边形BCQM是平行四边形，
∴BM=CQ．
∵CP=CQ，∴BM=CP．
∵AM∥BC，∴∠AMB=∠PBC．
∵∠A=∠BPC=90°，
∴△BAM∽△CPB，
∴$\frac{BM}{CB}$=$\frac{BA}{CP}$，
∴BM•CP=AB•BC，
∴BM²=AB•BC；

（3）△MBC内切圆的半径的最大值为$\frac{3}{2}$．
提示：延长BA到点B′，使得AB′=AB，连接MB′，如图3，

则有AM垂直平分BB′，
∴MB′=MB，
∴MB+MC=MB′+MC．
根据两点之间线段最短可得：当B′、M、C三点共线时，MB+MC取到最小值，最小值为B′C长．
∵B′B=2AB=8，BC=6，
∴B′C=$\sqrt{BB{′}^{2}+B{C}^{2}}$=10，
∴MB+MC取到最小值为10．
设△MBC内切圆的半径为r，
∵S_△MBC=$\frac{1}{2}$BC•AB=$\frac{1}{2}$×6×4=12，
且S_△MBC=$\frac{1}{2}$（MB+MC+BC）•r，
∴$\frac{1}{2}$（MB+MC+BC）•r=12，
∴r=$\frac{24}{MB+MC+BC}$．
当MB+MC取最小值10时，MB+MC+BC取最小值16，
此时r取到最大值，最大值为$\frac{24}{16}$=$\frac{3}{2}$．

点评 本题主要考查了矩形的性质、相似三角形的判定与性质、二次函数的最值性、全等三角形的判定与性质、垂直平分线的性质、等腰三角形的性质、平行四边形的判定与性质、两点之间线段最短、勾股定理、三角形的面积公式等知识，考查的知识面比较广，综合性比较强．利用平行线和线段的中点构造全等三角形是解决第（1）小题的关键，证到BM=CQ=CP是解决第（2）小题的关键，利用等积法（三角形的面积既等于底边与底边上高的乘积的一半，又等于三角形的周长与内切圆半径的乘积的一半）是解决第（3）小题的关键．