
分析 (1)根据公式法,可得方程的解;
(2)根据分式的加减,可得答案.
解答 解:(1)a=1,b=4,c=-1,
∵△=42-4×1×(-1)=20
∴$x=\frac{{-4±\sqrt{20}}}{2}$,
x1=-2+$\sqrt{5}$,x2=-2-$\sqrt{5}$;
(2)原式=$\frac{2a}{(a+3)(a-3)}-\frac{a-3}{(a+3)(a-3)}$
=$\frac{2a-(a-3)}{(a+3)(a-3)}$
=$\frac{a+3}{(a+3)(a-3)}$
=$\frac{1}{a-3}$.
点评 本题考查了解一元二次方程,(1)先确定a、b、c的值,再利用根的判别式,最后套用公式;(2)利用分式的加减,先通分再加减.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
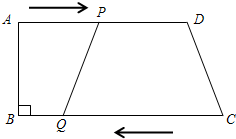 如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x<\frac{2}{3}$ | B. | $x<\frac{3}{2}$ | C. | $x≥\frac{2}{3}$ | D. | $x≥\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com