练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是

    A.（0，0）B.（0，1）C.（0，2）D.（0，3）

    【答案】D

    【解析】

    解：作B点关于y轴对称点B′点，连接AB′，交y轴于点C′，
    此时△ABC的周长最小，

    ∵点A、B的坐标分别为（1，4）和（3，0），
    ∴B′点坐标为：（-3，0），则OB′=3

    过点A作AE垂直x轴，则AE=4，OE=1
    则B′E=4，即B′E=AE，∴∠EB′A=∠B′AE，
    ∵C′O∥AE，
    ∴∠B′C′O=∠B′AE，

    ∴∠B′C′O=∠EB′A

    ∴B′O=C′O=3，
    ∴点C′的坐标是（0，3），此时△ABC的周长最小．
    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算题：

    （1）8+(-10)+(-2)-(-5)

    （2）

    （3）

    （4）-

    （5）

    （6）

    （7）（）×4

    （8）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

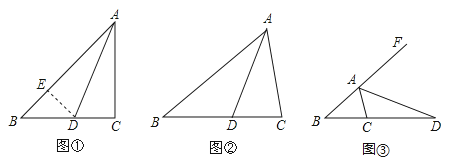
    【题目】在△ABC中，∠ACB=2∠B，（1）如图①，当∠C=90°，AD为∠ABC的角平分线时，在AB上截取AE=AC，连接DE，易证AB=AC+CD．请证明AB=AC+CD；

    （2）①如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？请直接写出你的结论，不要求证明；

    ②如图③，当∠C≠90°，AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读理解）

    点A、B、C为数轴上三点，如果点C在A、B之间且到A的距离是点C到B的距离3倍，那么我们就称点C是{A，B}的奇点．

    例如，如图1，点A表示的数为﹣3，点B表示的数为1．表示0的点C到点A的距离是3，到点B的距离是1，那么点C是{A，B}的奇点；又如，表示﹣2的点D到点A的距离是1，到点B的距离是3，那么点D就不是{A，B}的奇点，但点D是{B，A}的奇点．

    （知识运用）

    如图2，M、N为数轴上两点，点M所表示的数为﹣3，点N所表示的数为5．

    （1）数　　　　 所表示的点是{M，N}的奇点；数　　　　 所表示的点是{N，M}的奇点；

    （2）如图3，A、B为数轴上两点，点A所表示的数为﹣50，点B所表示的数为30．现有一动点P从点B出发向左运动，当P点运动到数轴上的什么位置时，P、A和B中恰有一个点为其余两点的奇点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，P是线段AB上的一点，在AB的同侧作△APC和△BPD，使PC=PA，PD=PB，∠APC=∠BPD，连接CD，点E、F、G、H分别是AC、AB、BD、CD的中点，顺次连接E、F、G、H．

    （1）猜想四边形EFGH的形状，直接回答，不必说明理由；

    （2）当点P在线段AB的上方时，如图2，在△APB的外部作△APC和△BPD，其他条件不变，（1）中的结论还成立吗？说明理由；

    （3）如果（2）中，∠APC=∠BPD=90°，其他条件不变，先补全图3，再判断四边形EFGH的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图的七边形ABCDEFG中，AB、ED的延长线相交于O点．若图中∠1、∠2、∠3、∠4的外角的角度和为220°，则∠BOD的度数是（　　）

    A. 400 B. 450 C. 500 D. 600

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC为等边三角形，点E、F分别在BC和AB上，且CE=BF，AE与CF相交于点H.

    （1）求证：△ACE≌△CBF；

    （2）求∠CHE的度数；

    （3）如图2，在图1上以AC为边长再作等边△ACD，将HE延长至G使得HG=CH，连接HD与CG，求证：HD=AH+CH

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四川苍溪小王家今年红心猕猴桃喜获丰收，采摘上市20天全部销售完，小王对销售情况进行跟踪记录，并将记录情况绘制成图象，日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图（1）所示，红星猕猴桃的价格z（单位：元/千克）与上市时间x（天）的函数关系式如图（2）所示．

    （1）观察图象，直接写出日销售量的最大值；

    （2）求小王家红心猕猴桃的日销量y与上市时间x的函数解析式；并写出自变量的取值范围．

    （3）试比较第6天和第13天的销售金额哪天多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】填写推理理由

    如图：EF∥AD，∠1＝∠2，∠BAC＝70°，把求∠AGD的过程填写完整.

    证明：∵EF∥AD

    ∴∠2＝ ( )

    又∵∠1＝∠2

    ∴∠1＝∠3（ ）

    ∴AB∥ ( )

    ∴∠BAC＋ ＝180°( )

    又∵∠BAC＝70°

    ∴∠AGD＝

    查看答案和解析>>

    同步练习册答案