
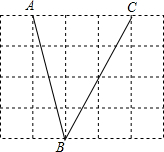
 如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请只用一把无刻度直尺作图:①线段AB上画出点P,使AP=$\frac{\sqrt{17}}{3}$;②作△ABC,使点C落在格点上,并且使△ABC的面积为6(只作一个);③作线段CD=$\frac{12\sqrt{17}}{17}$.
如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请只用一把无刻度直尺作图:①线段AB上画出点P,使AP=$\frac{\sqrt{17}}{3}$;②作△ABC,使点C落在格点上,并且使△ABC的面积为6(只作一个);③作线段CD=$\frac{12\sqrt{17}}{17}$.分析 ①连接MN交AB于点P,点P即为所求;由勾股定理求出AB,由平行线得出△AMP∽△BNP,得出对应边成比例,求出AP即可;
②由△ABC的面积=6=$\frac{1}{2}$×4×3,得出AC=3,画出图形即可;
③连接CF,交AB于D,CD即为所求;由SAS证明△ABE≌△CFG,得出∠BAE=∠FCG,证出∠ADC=90°,得出CD⊥AB,由△ABC的面积求出CD即可.
解答 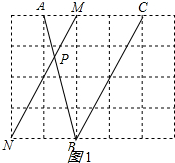 解:①如图1所示:
解:①如图1所示:
连接MN交AB于点P,点P即为所求;理由如下:
由勾股定理得:AB=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
∵AM∥BN,
∴△AMP∽△BNP,
∴$\frac{AP}{BP}=\frac{AM}{BN}=\frac{1}{2}$,
∴$\frac{AP}{AB}=\frac{1}{3}$,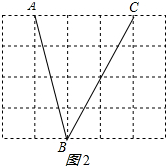
∴AP=$\frac{1}{3}$AB=$\frac{\sqrt{17}}{3}$;
②如图2所示:
③如图3所示:
连接CF,交AB于D,CD即为所求;理由如下:
在△ABE和△CFG中,
$\left\{\begin{array}{l}{BE=FG=1}&{\;}\\{∠AEB=∠CGF=90°}&{\;}\\{AE=CG=4}&{\;}\end{array}\right.$,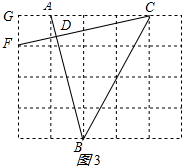 ∴△ABE≌△CFG(SAS),
∴△ABE≌△CFG(SAS),
∴∠BAE=∠FCG,
∴∠FCG+∠BAC=∠BAE+∠BAC=90°,
∴∠ADC=90°,
∴CD⊥AB,
∵△ABC的面积=$\frac{1}{2}$×3×4=$\frac{1}{2}$AB•CD,
∴CD=$\frac{12\sqrt{17}}{17}$.
点评 本题考查了正方形的性质、勾股定理、全等三角形的判定与性质、相似三角形的判定与性质、三角形面积的计算等知识;本题有一定难度,证明三角形相似和三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | $\frac{22}{7}$ | C. | π | D. | ($\sqrt{3}$)0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | ±1 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 3$\sqrt{5}$-$\sqrt{5}$=2 | C. | $\sqrt{2}×\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{18}$÷$\sqrt{3}$=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
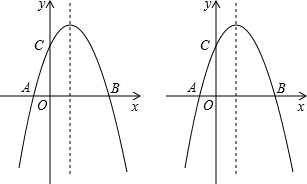 抛物线y=-x2+bx+c经过点A(-1,0)和C(0,3).
抛物线y=-x2+bx+c经过点A(-1,0)和C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
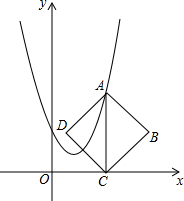 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )| A. | (2,2),(3,5) | B. | (2,2),(4,10) | C. | (3,5),(4,10) | D. | (2,2),(4,10),(6,26) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
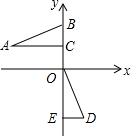 如图,在平面直角坐标系xOy中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系xOy中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C顺时针旋转90°,再向下平移3 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| C. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 321×103米 | B. | 32.1×103米 | C. | 3.21×104米 | D. | 3.21×103米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com