
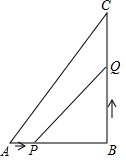
 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点 A 开始沿边AB向B 以lcm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q分别同时从A、B出发.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点 A 开始沿边AB向B 以lcm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q分别同时从A、B出发.分析 (1)设经过x秒,△PBQ的面积等于8cm2,先用含x的代数式分别表示BP和BQ的长度,再代入三角形面积公式,列出方程,即可将时间求出;
(2)利用勾股定理列出方程求解即可;
(3)利用相似三角形对应边的比相等列出方程求解即可.
解答 解:(1)设经过x秒,△PBQ的面积等于8cm2.
∵AP=1•x=x,BQ=2x,
∴BP=AB-AP=6-x,
∴S△PBQ=$\frac{1}{2}$×BP×BQ=$\frac{1}{2}$×(6-x)×2x=8,
∴x2-6x+8=0,
解得:x=2或4,
即经过2秒或4秒,△PBQ的面积等于8cm2;
(2)由(1)得:(6-x)2+(2x)2=(3$\sqrt{5}$)2,
解得:x=3或x=-$\frac{3}{5}$.
答:经过3秒PQ的长为3$\sqrt{5}$cm;
(3)当△ABC∽△PBQ时,
$\frac{PB}{AB}=\frac{BQ}{BC}$,
即:$\frac{6-x}{6}=\frac{2x}{8}$,
解得:x=2.4,;
当△ABC∽△QBP时,
$\frac{PB}{BC}=\frac{BQ}{AB}$,
即:$\frac{6-x}{8}=\frac{2x}{6}$,
解得:x=$\frac{18}{11}$.
故2.4秒或$\frac{18}{11}$秒时△ABC与以点P、B、Q为顶点的三角形相似.
点评 本题考查了一元二次方程的应用及相似三角形的判定.关键是用含时间的代数式准确表示BP和BQ的长度,再根据三角形的面积公式列出一元二次方程,进行求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形框(如图所示中阴影部分)已知铺这个框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?
一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形框(如图所示中阴影部分)已知铺这个框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
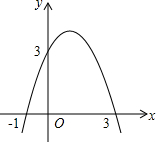 二次函数y=-x2+2x+3的图象如图所示,在x轴上方,且平行于x轴的直线与该二次函数的图象交于M,N两点,在x轴上取点Q,使△MNQ为等腰直角三角形,请你写出所有符合的点Q的坐标(1,0)或(2-$\sqrt{5}$,0)或($\sqrt{5}$,0).
二次函数y=-x2+2x+3的图象如图所示,在x轴上方,且平行于x轴的直线与该二次函数的图象交于M,N两点,在x轴上取点Q,使△MNQ为等腰直角三角形,请你写出所有符合的点Q的坐标(1,0)或(2-$\sqrt{5}$,0)或($\sqrt{5}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
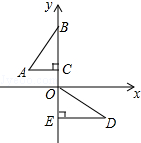 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移2 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移2 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移6 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
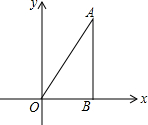 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com